
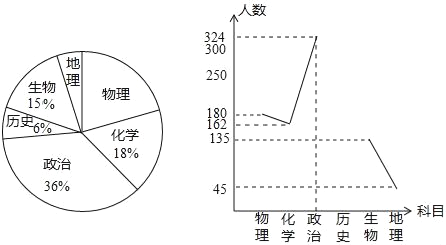
【题目】某校对九年级学生进行随机抽样调查,被抽到的学生从物理、化学、生物、地理、历史和政治这六科中选出自己最喜欢的科目,将调查数据汇总整理后,绘制了两幅不同的统计图,请你根据图中信息解答下列问题:
(1)被抽查的学生共有多少人?求出地理学科所在扇形的圆心角;
(2)将折线统计图补充完整;
(3)若该校九年级学生约2000人请你估算喜欢物理学科的人数.
【答案】(1)900人,18°;(2)补图见解析;(3)400人
【解析】
(1)根据政治科目的人数及其所占百分比可得总人数,依据地理学科的人数所占的百分比,即可得到其所在扇形的圆心角;(2)总人数乘以历史科目的百分比可得其人数,从而补全折线图;(3)总人数乘以样本中物理科目人数所占比例即可得.
解:(1)由图知把政治作为首选的324人,占抽查总人数的百分比为36%,
抽查人数为:324÷36%=900人,
地理学科所在扇形的圆心角=360°×![]() =18°;
=18°;
答:被抽查的学生共有900人,地理学科所在扇形的圆心角为18°.
(2)本次调查中,首选历史科目的人数为900×6%=54人,
补全折线图如下:
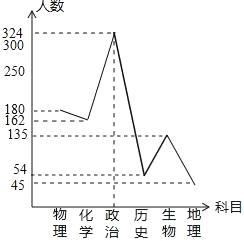
(3)2000×![]() =400,
=400,
答:估计喜欢物理学科的人数为400人.


科目:初中数学 来源: 题型:
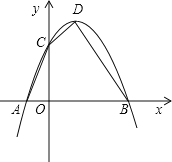
【题目】已知:如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,3),与x轴交于A、B两点,点A的坐标为(-1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)设点P是在第一象限内抛物线上的一个动点,求使与四边形ACDB面积相等的四边形ACPB的点P的坐标;
(3)求△APD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的袋子中装有4个相同的小球,它们除颜色外无其它差别,把它们分别标号:1、2、3、4,
(1)随机摸出一个小球后,放回并摇匀,再随机摸出一个,用列表或画树状图的方法求出“两次取的球标号相同”的概率
(2)随机摸出两个小球,直接写出“两次取出的球标号和等于4”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:是某出租车单程收费y(元)与行驶路程x(千米)之间的函数关系图象,根据图象回答下列问题:

(1)当行使8千米时,收费应为 元;
(2)从图象上你能获得哪些信息?(请写出2条)
① ________
②____________________________
(3)求出收费y(元)与行使x(千米)(x≥3)之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
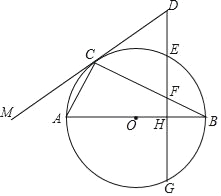
【题目】已知:△ABC内接于⊙O,AB是⊙O的直径,作EG⊥AB于H,交BC于F,延长GE交直线MC于D,且∠MCA=∠B,求证:
(1)MC是⊙O的切线;
(2)△DCF是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】细心的小明发现,一元二次方程ax2+bx+c=0(a≠0)根与系数之间的“秘密”关系.
(1)当x=1时有a+b+c=0,当x=﹣1时有a﹣b+c=0.若9a+c=3b,求x;
(2)若2a+b=0,3a+c=0,写出满足条件的一个一元二次方程,并求另一个根;
(3)当老师写出方程2x2﹣3x﹣1=0,要求不解方程判断根的情况时,小明立即回答,有两个不相等的实数根.据此,你能根据一元二次方程系数a、b、c的符号以及相互之间的数量关系,写出一些关于一元二次方程ax2+bx+c=0(a≠0)根与系数之间的规律吗?请写一写(至少两条).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形![]() 的顶点
的顶点![]() 是坐标原点,点
是坐标原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() ,
,![]() 分别为四边形
分别为四边形![]() 边上的动点,动点
边上的动点,动点![]() 从点
从点![]() 开始,以每秒1个单位长度的速度沿
开始,以每秒1个单位长度的速度沿![]() 路线向终点
路线向终点![]() 匀速运动,动点
匀速运动,动点![]() 从
从![]() 点开始,以每秒2个单位长度的速度沿
点开始,以每秒2个单位长度的速度沿![]() 路线向终点
路线向终点![]() 匀速运动,点
匀速运动,点![]() 、
、![]() 同时从
同时从![]() 点出发,当其中一点到达终点后,另一点也随之停止运动.设动点运动的时间为
点出发,当其中一点到达终点后,另一点也随之停止运动.设动点运动的时间为![]() 秒(
秒(![]() ),
),![]() 的面积为
的面积为![]() .
.
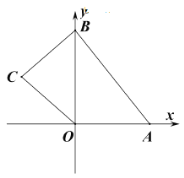
(1)填空:![]() 的长是________;
的长是________;
(2)当![]() 时,求
时,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)若![]() ,请直接写出此时
,请直接写出此时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班准备选一名学生参加数学史知识竞赛,现统计了两名选手本学期的五次测试 成绩:甲:83,80,90,87, 85; 乙:78,92,82,89,84.
(1)请根据上面的数据完成下表:
极差 | 平均数 | 方差 | |
甲 | 10 | ________ | ________ |
乙 | _________ | 85 | 24.8 |
(2)请你推选出一名参赛选手,并用所学的统计知识说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,BC=CD,∠C=2∠BAD.
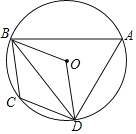
(1)求∠BOD的度数;
(2)求证:四边形OBCD是菱形;
(3)若⊙O的半径为r,∠ODA=45°,求△ABD的面积(用含r的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com