
【题目】已知:△ABC内接于⊙O,AB是⊙O的直径,作EG⊥AB于H,交BC于F,延长GE交直线MC于D,且∠MCA=∠B,求证:
(1)MC是⊙O的切线;
(2)△DCF是等腰三角形.
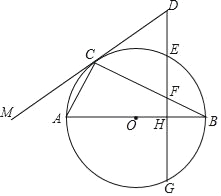
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)连接OC,如图,利用圆周角定理得到∠2+∠3=90°,再证明∠1=∠3得到∠1+∠2=90°,即∠OCM=90°,然后根据切线的判定定理可得到结论;
(2)利用EG⊥AB得到∠B+∠BFH=90°,利用对顶角相等得到∠4+∠B=90°,而根据切线的性质得到∠5+∠3=90°,从而得到∠4=∠5,然后根据等腰三角形的判定定理可得结论.
证明:(1)连接OC,如图,
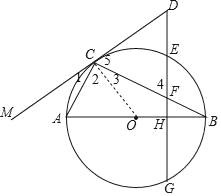
∵AB是⊙O的直径,
∴∠ACB=90°,
即∠2+∠3=90°,
∵OB=OC,
∴∠B=∠3,
而∠1=∠B,
∴∠1=∠3,
∴∠1+∠2=90°,
即∠OCM=90°,
∴OC⊥CM,
∴MC是⊙O的切线;
(2)∵EG⊥AB,
∴∠B+∠BFH=90°,
而∠BFH=∠4,
∴∠4+∠B=90°,
∵MD为切线,
∴OC⊥CD,
∴∠5+∠3=90°,
而∠3=∠B,
∴∠4=∠5,
∴△DCF是等腰三角形.


科目:初中数学 来源: 题型:
【题目】如图,直线y1=﹣x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A(1,m),这两条直线分别与x轴交于B,C两点.
交于点A(1,m),这两条直线分别与x轴交于B,C两点.
(1)求y与x之间的函数关系式;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
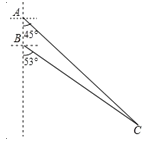
【题目】如图所示,我国两艘海监船 A,B 在南海海域巡逻,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船 C,此时,B 船在A 船的正南方向 15 海里处,A 船测得渔船 C 在其南偏东 45°方向,B 船测得渔船 C 在其南偏东 53°方向,已知 A 船的航速为 30 海里/小时,B 船的航速为 25 海里/小时,问 C 船至少要等待多长时间才能得到救援?(参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈ 4 ,
,tan53°≈ 4 ,![]() 1.41 )
1.41 )
查看答案和解析>>
科目:初中数学 来源: 题型:
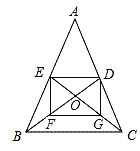
【题目】如图,△ABC的中线BD,CE交于点O,F,G分别是BO,CO的中点.
(1)填空:四边形DEFG是 四边形.
(2)若四边形DEFG是矩形,求证:AB=AC.
(3)若四边形DEFG是边长为2的正方形,试求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
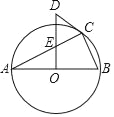
【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径,OD⊥AB,与AC交于点E,∠D=2∠A.
(1)求证:CD是⊙O的切线;
(2)求证:DE=DC;
(3)若OD=5,CD=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
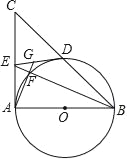
【题目】已知:AB为⊙O的直径,AB=AC,BC交⊙O于点D,DE⊥AC于E.
(1)求证:DE为⊙O的切线;
(2)连接BE交圆于F,连AF并延长ED于G,若GE=2,AF=3,求∠EAF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
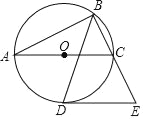
【题目】如图,以△ABC的边AC为直径的⊙O恰为△ABC的外接圆,∠ABC的平分线交⊙O于点D,过点D作DE∥AC交BC的延长线于点E.
(1)求证: DE是⊙O的切线;
(2)若AB=2![]() ,BC=
,BC=![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
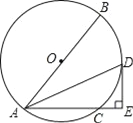
【题目】如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线.
(2)求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com