
【题目】如图,直线y1=﹣x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A(1,m),这两条直线分别与x轴交于B,C两点.
交于点A(1,m),这两条直线分别与x轴交于B,C两点.
(1)求y与x之间的函数关系式;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.

【答案】(1)![]() ;(2)x>1;(3)P(﹣
;(2)x>1;(3)P(﹣![]() ,0)或(
,0)或(![]() ,0)
,0)
【解析】
(1)求得A(1,3),把A(1,3)代入双曲线y=![]() ,可得y与x之间的函数关系式;
,可得y与x之间的函数关系式;
(2)依据A(1,3),可得当x>0时,不等式![]() x+b>
x+b>![]() 的解集为x>1;
的解集为x>1;
(3)分两种情况进行讨论,AP把△ABC的面积分成1:3两部分,则CP=![]() BC=
BC=![]() ,或BP=
,或BP=![]() BC=
BC=![]() ,即可得到OP=3﹣
,即可得到OP=3﹣![]() =
=![]() ,或OP=4﹣
,或OP=4﹣![]() =
=![]() ,进而得出点P的坐标.
,进而得出点P的坐标.
(1)把A(1,m)代入y1=﹣x+4,可得m=﹣1+4=3,
∴A(1,3),
把A(1,3)代入双曲线y=![]() ,可得k=1×3=3,
,可得k=1×3=3,
∴y与x之间的函数关系式为:y=![]() ;
;
(2)∵A(1,3),
∴当x>0时,不等式![]() x+b>
x+b>![]() 的解集为:x>1;
的解集为:x>1;
(3)y1=﹣x+4,令y=0,则x=4,
∴点B的坐标为(4,0),
把A(1,3)代入y2=![]() x+b,可得3=
x+b,可得3=![]() +b,
+b,
∴b=![]() ,
,
∴y2=![]() x+
x+![]() ,
,
令y2=0,则x=﹣3,即C(﹣3,0),
∴BC=7,
∵AP把△ABC的面积分成1:3两部分,
∴CP=![]() BC=
BC=![]() ,或BP=
,或BP=![]() BC=
BC=![]()
∴OP=3﹣![]() =
=![]() ,或OP=4﹣
,或OP=4﹣![]() =
=![]() ,
,
∴P(﹣![]() ,0)或(
,0)或(![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】阅读探索题:
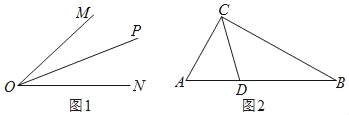
(1)如图1,OP是∠MON的平分线,以O为圆心任意长为半径作弧,分别交射线ON、OM于C、B两点,在射线OP上任取一点A(点O除外),连接AB、AC.求证:△AOB≌△AOC.
(2)请你参考以上方法,解答下列问题:
如图2,在 Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB,试判断BC和AC、AD之间的数量关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
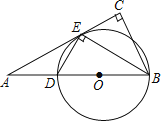
【题目】如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,作ED⊥EB交AB于点D,⊙O是△BED的外接圆.
(1)求证:AC是⊙O的切线;
(2)已知⊙O的半径为2.5,BE=4,求BC,AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
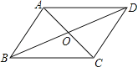
A.AB∥CD,AD∥BCB.OA=OC,OB=OD
C.AD=BC,AB∥CDD.AB=CD,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC与BD交于点M,点F在AD上,AF=6cm,BF=12cm,∠FBM=∠CBM,点E是BC的中点,若点P以1cm/s秒的速度从点A出发,沿AD向点F运动;点Q同时以2cm/秒的速度从点C出发,沿CB向点B运动,点P运动到F点时停止运动,点Q也同时停止运动,当点P运动__秒时,以P、Q、E、F为顶点的四边形是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:常用的分解因式方法有提公因式、公式法等,但有的多项式只有上述方法就无法分解,如x2﹣4y2+2x﹣4y,细心观察这个式子会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式,过程为:
x2﹣4y2+2x﹣4y
=(x2﹣4y2)+(2x﹣4y)
=(x+2y)(x﹣2y)+2(x﹣2y)
=(x﹣2y)(x+2y+2)
这种分解因式的方法叫分组分解法,利用这种方法解决下列问题:
(1)分解因式:x2﹣6xy+9y2﹣3x+9y
(2)△ABC的三边a,b,c满足a2﹣b2﹣ac+bc=0,判断△ABC的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
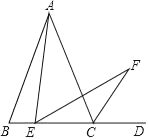
【题目】如图,在△ABC中,AB=AC=2![]() ,BC=4.点E为BC边上一动点,连接AE,作∠AEF=∠B,EF与△ABC的外角∠ACD的平分线交于点F.当EF⊥AC时,EF的长为_______.
,BC=4.点E为BC边上一动点,连接AE,作∠AEF=∠B,EF与△ABC的外角∠ACD的平分线交于点F.当EF⊥AC时,EF的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙二人做某种机械零件,已知每小时甲比乙少做8个,甲做120个所用的时间与乙做150个所用的时间相等.
(1)甲、乙二人每小时各做零件多少个?
(2)甲做几小时与乙做4小时所做机械零件数相等?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com