
����Ŀ��ϸ�ĵ�С�����֣�һԪ���η���ax2+bx+c��0��a��0������ϵ��֮��ġ����ܡ���ϵ��
��1����x��1ʱ��a+b+c��0����x����1ʱ��a��b+c��0����9a+c��3b����x��
��2����2a+b��0��3a+c��0��д������������һ��һԪ���η��̣�������һ������
��3������ʦд������2x2��3x��1��0��Ҫ�ⷽ���жϸ������ʱ��С�������ش�����������ȵ�ʵ�������ݴˣ����ܸ���һԪ���η���ϵ��a��b��c�ķ����Լ��֮���������ϵ��д��һЩ����һԪ���η���ax2+bx+c��0��a��0������ϵ��֮��Ĺ�������дһд��������������
���𰸡���1��x����3��2��x2-3x-4=0;x2��4����3��������.
��������
��1��ֱ��ͨ���۲�Աȿɵó���.
��2���������֪һ����Ϊ-1���پ�������.
��3�����ݸ����б�ʽ��Τ�ﶨ�����.
��1����9a+c��3b��
��9a��3b+c��0��
��x����3��
��2����![]()
�ک��ٵã�a��b+c��0��
��x����1��
���������ķ��̿���Ϊ��x2��3x��4��0��
��x��4����x+1����0��
x1��4��x2����1��
��3��2x2��3x��1��0��
��Ϊa��2��c����1����֪��ac��0��
�����b2��4ac��0��
����һԪ���η���ϵ��a��b��c�ķ����Լ��֮���������ϵ���У��ٵ�a��c���ʱ������0����������������ȵ�ʵ����
���跽��ax2+bx+c��0������x1��x2������x1+x2��![]() ��x1x2��
��x1x2��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
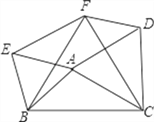
����Ŀ����ͼ������ABC������Ϊ�߷ֱ����ȱ���ACD����ABE����BCF��
��1����֤����EBF�ա�DFC��
��2����֤���ı���AEFD��ƽ���ı��Σ�
��3���١�ABC����_____________________ʱ���ı���AEFD�����Ρ�������֤����
�ڡ�ABC����_______________________ʱ���ı���AEFD�Ǿ��Ρ�������֤����
�ۡ�ABC����_______________________ʱ���ı���AEFD�������Ρ�������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
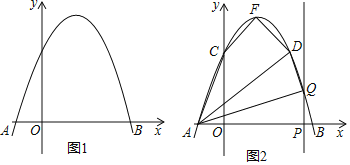
����Ŀ����ͼ1��������y=ax2+bx+3��x���ڵ�A����1��0���͵�B��3��0����
��1���������������Ӧ�ĺ�������ʽ��
��2����ͼ2������������y�ύ�ڵ�C������ΪF����D��2��3���ڸ��������ϣ�
�����ı���ACFD�������
�ڵ�P���߶�AB�ϵĶ��㣨��P�����A��B�غϣ�������P��PQ��x�ύ���������ڵ�Q������AQ��DQ������AQD��ֱ��������ʱ������������������ĵ�Q�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ֱ�������֩�1����2��0��1��2��3��4�Ŀ�Ƭ�������ֲ�ͬ������ȫ����ͬ���ֽ����DZ��泯�ϣ�ϴ�Ⱥ���������ȡһ�ţ��ǿ�Ƭ�ϵ�����Ϊm����ʹ����x�ķ���x2��2��m��1��x+m2��3m��0��ʵ�������Ҳ���ʽ��![]() ��ĸ�����_____��
��ĸ�����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
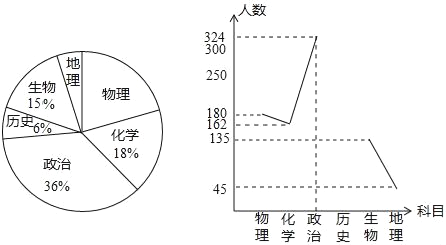
����Ŀ��ijУ�Ծ��꼶ѧ����������������飬���鵽��ѧ������������ѧ�������������ʷ��������������ѡ���Լ���ϲ���Ŀ�Ŀ�����������ݻ�������������������ͬ��ͳ��ͼ���������ͼ����Ϣ����������⣺
��1��������ѧ�����ж����ˣ��������ѧ���������ε�Բ�Ľǣ�
��2��������ͳ��ͼ����������
��3������У���꼶ѧ��Լ2000���������ϲ������ѧ�Ƶ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��4��3���Ƿ���������y=![]() �ڵ�һ����ͼ����һ�㣬����OA����A��AB��x�ᣬ��ȡAB=OA��B��A�Ҳࣩ������OB��������������y=
�ڵ�һ����ͼ����һ�㣬����OA����A��AB��x�ᣬ��ȡAB=OA��B��A�Ҳࣩ������OB��������������y=![]() ��ͼ���ڵ�P��
��ͼ���ڵ�P��
��1����������y=![]() �ı���ʽ��
�ı���ʽ��
��2�����B�����ꣻ
��3������OAP�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ǵȱ������Σ�CE�����ƽ���ߣ���D��AC�ϣ�����BD���ӳ���CE���ڵ�E��
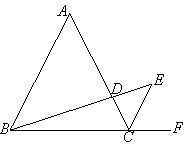
��1����֤����ABD�ס�CED��
��2����AB��6��AD��2CD����BE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Գ���Ϊֱ��x����1��������y��ax2+bx+c��a��0����x���ཻ��A��B���㣮
��1������A������Ϊ����4��0�������B�����꣮
��2������֪a��1����A������Ϊ����3��0����CΪ��������y��Ľ��㣮
������P���������ϣ���S��POC��4S��BOC�����P�����ꣻ
�����Q���߶�AC�ϵĶ��㣬��QD��x�ύ�������ڵ�D�����߶�QD���ȵ����ֵ��
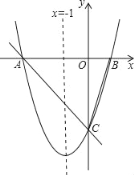
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽƬABCD��AD=4��AB=3�������E�ڱ�BC�ϣ���ֽƬ��AE�۵���ʹ��B���ڵ�F��������FC������EFC��ֱ��������ʱ����ôBE�ij�Ϊ_____��
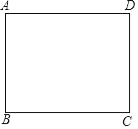
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com