
【题目】如图,A(4,3)是反比例函数y=![]() 在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=
在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=![]() 的图象于点P.
的图象于点P.
(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)求点B的坐标;
(3)求△OAP的面积.

【答案】(1)反比例函数解析式为y=![]() ;(2)点B的坐标为(9,3);(3)△OAP的面积=5.
;(2)点B的坐标为(9,3);(3)△OAP的面积=5.
【解析】(1)将点A的坐标代入解析式求解可得;
(2)利用勾股定理求得AB=OA=5,由AB∥x轴即可得点B的坐标;
(3)先根据点B坐标得出OB所在直线解析式,从而求得直线与双曲线交点P的坐标,再利用割补法求解可得.
(1)将点A(4,3)代入y=![]() ,得:k=12,
,得:k=12,
则反比例函数解析式为y=![]() ;
;
(2)如图,过点A作AC⊥x轴于点C,
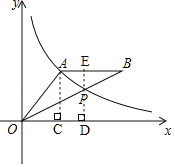
则OC=4、AC=3,
∴OA=![]() =5,
=5,
∵AB∥x轴,且AB=OA=5,
∴点B的坐标为(9,3);
(3)∵点B坐标为(9,3),
∴OB所在直线解析式为y=![]() x,
x,
由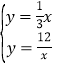 可得点P坐标为(6,2),(负值舍去),
可得点P坐标为(6,2),(负值舍去),
过点P作PD⊥x轴,延长DP交AB于点E,
则点E坐标为(6,3),
∴AE=2、PE=1、PD=2,
则△OAP的面积=![]() ×(2+6)×3﹣
×(2+6)×3﹣![]() ×6×2﹣
×6×2﹣![]() ×2×1=5.
×2×1=5.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】计算:
(1)![]() ﹣
﹣![]() +|
+|![]() ﹣3|
﹣3|
(2)x2x4﹣(﹣3x2)3
(3)(m+1)(m﹣3)﹣(m+2)2+(m+2)(m﹣2)
(4)20142﹣2013×2015(用公式计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“元旦”期间,平价商场对该商场商品进行如下的优惠促销活动:
打折前一次性购物总金额 | 优惠措施 |
小于等于 400 元 | 不优惠 |
超过 400 元,但不超过 600元 | 按售价打九折 |
超过 600 元 | 其中 600 元部分八折优惠,超过 600 元的部分打六折优惠 |
按上述优惠条件,若小华一次性购买售价为 80 元/件的商品 n 件时,实际付款 504 元, 则 n=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠B=90°,点P从点A出发,沿A→B→C以1cm/s的速度运动.设△APC的面积为s(m),点P的运动时间为t(s),变量S与t之间的关系如图2所示,则在运动过程中,S的最大值是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图E是平行四边形![]() 边BC上一点,且
边BC上一点,且![]() ,连接AE,并延长AE与DC的延长线交于点F,
,连接AE,并延长AE与DC的延长线交于点F, ![]() .
.
(1)请判断![]() 的形状,并说明理由;
的形状,并说明理由;
(2)求![]() 的各内角的大小.
的各内角的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD是菱形,AD=5,过点D作AB的垂线DH,垂足为H,交对角线AC于M,连接BM,且AH=3.
(1)求证:DM=BM;
(2)求MH的长;
(3)如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式;
(4)在(3)的条件下,当点P在边AB上运动时是否存在这样的 t值,使∠MPB与∠BCD互为余角,若存在,则求出t值,若不存,在请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以点A为顶点作两个等腰直角三角形(△ABC,△ADE),如图1所示放置,使得一直角边重合,连接BD,CE.

(1)说明BD=CE;
(2)延长BD,交CE于点F,求∠BFC的度数;
(3)若如图2放置,上面的结论还成立吗?请简单说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E 、F ,连结BD 、DP ,BD与CF相交于点H. 给出下列结论:①△BDE ∽△DPE;② ![]() ;③DP 2=PH ·PB; ④
;③DP 2=PH ·PB; ④ ![]() . 其中正确的是( ).
. 其中正确的是( ).
A.①②③④
B.①②④
C.②③④
D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
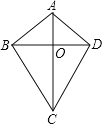
【题目】如图,在四边形ABCD中,AB=AD,CB=CD,对角线AC,BD相交于点O,下列结论中:①∠ABC=∠ADC;②AC与BD相互平分;③AC,BD分别平分四边形ABCD的两组对角;④四边形ABCD的面积S=![]() ACBD.
ACBD.
(1)写出正确结论的序号;
(2)证明所有正确的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com