
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E 、F ,连结BD 、DP ,BD与CF相交于点H. 给出下列结论:①△BDE ∽△DPE;② ![]() ;③DP 2=PH ·PB; ④
;③DP 2=PH ·PB; ④ ![]() . 其中正确的是( ).
. 其中正确的是( ).
A.①②③④
B.①②④
C.②③④
D.①③④
【答案】D
【解析】解:∵△BPC是等边三角形,
∴BP=PC=BC,∠PBC=∠PCB=∠BPC=60°,
在正方形ABCD中,
∵AB=BC=CD,∠A=∠ADC=∠BCD=90°
∴∠ABE=∠DCF=30°,
∴∠CPD=∠CDP=75°,
∴∠PDE=15°,
∵∠PBD=∠PBC-∠HBC=60°-45°=15°,
∴∠EBD=∠EDP,
∵∠DEP=∠DEB,
∴△BDE∽△DPE;
故①正确;
∵PC=CD,∠PCD=30°,
∴∠PDC=75°,
∴∠FDP=15°,
∵∠DBA=45°,
∴∠PBD=15°,
∴∠FDP=∠PBD,
∵∠DFP=∠BPC=60°,
∴△DFP∽△BPH,
∴ ![]()
故②错误;
∵∠PDH=∠PCD=30°,
∵∠DPH=∠DPC,
∴△DPH∽△CDP,
∴ ![]() ,
,
∴PD2=PHCD,
∵PB=CD,
∴PD2=PHPB,
故③正确;
如图,过P作PM⊥CD,PN⊥BC,
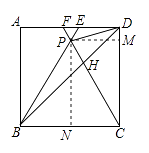
设正方形ABCD的边长是4,△BPC为正三角形,
∴∠PBC=∠PCB=60°,PB=PC=BC=CD=4,
∴∠PCD=30°
∴CM=PN=PBsin60°=4× ![]() ,PM=PCsin30°=2,
,PM=PCsin30°=2,
∵DE∥PM,
∴∠EDP=∠DPM,
∴∠DBE=∠DPM,
∴ ![]() ,
,
故④正确;
答案为:D。
①利用等边三角形的性质以及正方形的性质得出∠EPD=∠EDB=45°,再直接利用相似三角形的判定方法得出答案;
②利用等边三角形的性质结合正方形的性质证出△DFP∽△BPH,进而得出![]() ;
;
③利用相似三角形的判定与性质结合锐角三角函数关系得出答案;
④利用三角函数可转化 tan ∠ D B E=tan∠DPM,进而得出结果.


科目:初中数学 来源: 题型:
【题目】如图,A(4,3)是反比例函数y=![]() 在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=
在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=![]() 的图象于点P.
的图象于点P.
(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)求点B的坐标;
(3)求△OAP的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的面积为20cm2,对角线交于点O;以AB、AO为邻边做平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边做平行四边形AO1C2B;…依此类推,则平行四边形AO4C5B的面积为( )

A. ![]() cm2 B.
cm2 B. ![]() cm2 C.
cm2 C. ![]() cm2 D.
cm2 D. ![]() cm2
cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.
(1)按要求作图:
①画出△ABC关于原点O的中心对称图形△A1B1C1;
②画出将△ABC绕点O顺时针旋转90°得到△A2B2C2,
(2)按照(1)中②作图,回答下列问题:△A2B2C2中顶点A2坐标为 ,B2的坐标为

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)求该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性定客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司经销一种绿茶,每千克成本为50元.市场调查发现,在一段时间内,销售量w(千克)随销售单价x(元/千克)的变化而变化,具体关系式为 ![]() ,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为y(元),解答下列问题:
,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为y(元),解答下列问题:
(1)求y与x的关系式.
(2)当x取何值时,y的值最大?
(3)如果公司想要在这段时间内获得 ![]() 元的销售利润,销售单价应定为多少元?
元的销售利润,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=45°.若AD平分∠BAC交BC于D,BE⊥AC于E,且交A于O,连接OC.则下列说法中正确的是( )①AD⊥BC;②OC平分BE;③OE=CE;④△ACD≌△BCE;⑤△OCE的周长=AC的长度
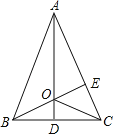
A.①②③B.②④⑤C.①③⑤D.①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣2x﹣3.
(1)该二次函数图象的对称轴为;
(2)判断该函数与x轴交点的个数,并说明理由;
(3)下列说法正确的是(填写所有正确说法的序号)
①顶点坐标为(1,﹣4);
②当y>0时,﹣1<x<3;
③在同一平面直角坐标系内,该函数图象与函数y=﹣x2+2x+3的图象关于x轴对称.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com