
【题目】在△ABC中,AB=AC,∠BAC=45°.若AD平分∠BAC交BC于D,BE⊥AC于E,且交A于O,连接OC.则下列说法中正确的是( )①AD⊥BC;②OC平分BE;③OE=CE;④△ACD≌△BCE;⑤△OCE的周长=AC的长度
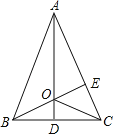
A.①②③B.②④⑤C.①③⑤D.①③④⑤
【答案】C
【解析】
①正确,利用等腰三角形的三线合一即可证明;②错误,证明OB=OC>OE即可判断;③正确,证明∠ECO=∠OBA=45°即可;④错误,缺少全等的条件;⑤正确,只要证明BE=AE,OB=OC,EO=EC即可判断.
解:∵AB=AC,AD平分∠BAC,
∴AD⊥BC,BD=CD,即①正确,
∴OB=OC,
∵BE⊥AC,
∵OC>OE,
∴OB>OE,即②错误,
∵∠ABC=∠ACB,∠OBC=∠OCB,BE⊥AC,
∴∠ABE=∠ACO=45°,
∴∠ECO=∠EOC=45°,
∴OE=CE,即③正确,
∵∠AEB=90°,∠ABE=45°,
∴AE=EB,
∴△OEC的周长=OC+OE+EC=OE+OB+EC=EB+EC=AE+EC=AC,即⑤正确,
无法判断△ACD≌△BCE,故④错误,
故选:C.


科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠B=90°,点P从点A出发,沿A→B→C以1cm/s的速度运动.设△APC的面积为s(m),点P的运动时间为t(s),变量S与t之间的关系如图2所示,则在运动过程中,S的最大值是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E 、F ,连结BD 、DP ,BD与CF相交于点H. 给出下列结论:①△BDE ∽△DPE;② ![]() ;③DP 2=PH ·PB; ④
;③DP 2=PH ·PB; ④ ![]() . 其中正确的是( ).
. 其中正确的是( ).
A.①②③④
B.①②④
C.②③④
D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,且交AD于点E,交BC于点F,连接BE,DF,且BE平分∠ABD.
①求证:四边形BFDE是菱形;
②直接写出∠EBF的度数.
(2)把(1)中菱形BFDE进行分离研究,如图2,G,I分别在BF,BE边上,且BG=BI,连接GD,H为GD的中点,连接FH,并延长FH交ED于点J,连接IJ,IH,IF,IG.试探究线段IH与FH之间满足的关系,并说明理由;
(3)把(1)中矩形ABCD进行特殊化探究,如图3,矩形ABCD满足AB=AD时,点E是对角线AC上一点,连接DE,作EF⊥DE,垂足为点E,交AB于点F,连接DF,交AC于点G.请直接写出线段AG,GE,EC三者之间满足的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
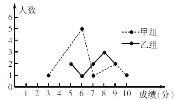
【题目】某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀. 为了解本次大赛的成绩,校团委随机抽取了甲、乙两组学生成绩作为样本进行统计,绘制了如下统计图表:
组别 | 平均数 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.8 | a | 3.76 | 90% | 30% |
乙组 | b | 7.5 | 1.96 | 80% | 20% |
(1)求出表中a,b的值;
(2)小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上面的表格判断,小英属于哪个组?
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组. 但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式及其验证过程:
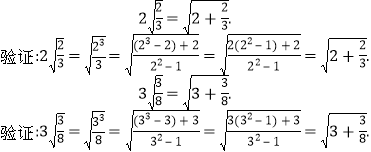
![]() 按照上述两个等式及其验证过程的基本思路,猜想
按照上述两个等式及其验证过程的基本思路,猜想![]() 的变形结果并进行验证;
的变形结果并进行验证;
![]() 针对上述各式反应的规律,写出用
针对上述各式反应的规律,写出用![]() 为任意自然数,且
为任意自然数,且![]() 表示的等式,并说明它成立.
表示的等式,并说明它成立.
查看答案和解析>>
科目:初中数学 来源: 题型:
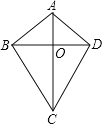
【题目】如图,在四边形ABCD中,AB=AD,CB=CD,对角线AC,BD相交于点O,下列结论中:①∠ABC=∠ADC;②AC与BD相互平分;③AC,BD分别平分四边形ABCD的两组对角;④四边形ABCD的面积S=![]() ACBD.
ACBD.
(1)写出正确结论的序号;
(2)证明所有正确的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,∠5=∠6,∠3=∠4,试说明AE∥BD,AD∥BC.请完成下列证明过程.
证明:
∵∠5=∠6,
∴AB∥CE( ),
∴∠3=__________
∵∠3=∠4,
∴∠4=∠BDC( ),
∴ ∥BD( ),
∴∠2= ( )
∵∠1=∠2,
∴∠1=______,
∴AD∥BC

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com