
【题目】如图1,抛物线y=ax2+bx+3交x轴于点A(﹣1,0)和点B(3,0).
(1)求该抛物线所对应的函数解析式;
(2)如图2,该抛物线与y轴交于点C,顶点为F,点D(2,3)在该抛物线上.
①求四边形ACFD的面积;
②点P是线段AB上的动点(点P不与点A、B重合),过点P作PQ⊥x轴交该抛物线于点Q,连接AQ、DQ,当△AQD是直角三角形时,求出所有满足条件的点Q的坐标.
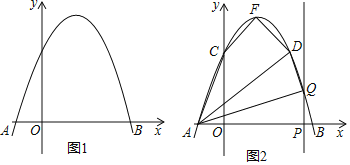
【答案】(1)y=﹣x2+2x+3;(2)①S四边形ACFD= 4;②Q点坐标为(1,4)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
此题涉及的知识点是抛物线的综合应用,难度较大,需要有很好的逻辑思维,解题时先根据已知点的坐标列方程求出函数解析式,然后再根据解析式和已知条件求出四边形的面积和点的坐标。
(1)由题意可得![]() ,解得
,解得![]() ,
,
∴抛物线解析式为y=﹣x2+2x+3;
(2)①∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴F(1,4),
∵C(0,3),D(2,3),
∴CD=2,且CD∥x轴,
∵A(﹣1,0),
∴S四边形ACFD=S△ACD+S△FCD=![]() ×2×3+
×2×3+![]() ×2×(4﹣3)=4;
×2×(4﹣3)=4;
②∵点P在线段AB上,
∴∠DAQ不可能为直角,
∴当△AQD为直角三角形时,有∠ADQ=90°或∠AQD=90°,
i.当∠ADQ=90°时,则DQ⊥AD,
∵A(﹣1,0),D(2,3),
∴直线AD解析式为y=x+1,
∴可设直线DQ解析式为y=﹣x+b′,
把D(2,3)代入可求得b′=5,
∴直线DQ解析式为y=﹣x+5,
联立直线DQ和抛物线解析式可得![]() ,解得
,解得![]() 或
或![]() ,
,
∴Q(1,4);
ii.当∠AQD=90°时,设Q(t,﹣t2+2t+3),
设直线AQ的解析式为y=k1x+b1,
把A、Q坐标代入可得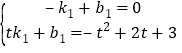 ,解得k1=﹣(t﹣3),
,解得k1=﹣(t﹣3),
设直线DQ解析式为y=k2x+b2,同理可求得k2=﹣t,
∵AQ⊥DQ,
∴k1k2=﹣1,即t(t﹣3)=﹣1,解得t=![]() ,
,
当t=![]() 时,﹣t2+2t+3=
时,﹣t2+2t+3=![]() ,
,
当t=![]() 时,﹣t2+2t+3=
时,﹣t2+2t+3=![]() ,
,
∴Q点坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
综上可知Q点坐标为(1,4)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
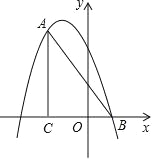
【题目】如图,在平面直角坐标系中,∠ACB=90°,OC=2BO,AC=6,点B的坐标为(1,0),抛物线y=﹣x2+bx+c经过A、B两点.
(1)求点A的坐标;
(2)求抛物线的解析式;
(3)点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE=![]() DE.
DE.
①求点P的坐标;
②在直线PD上是否存在点M,使△ABM为直角三角形?若存在,求出符合条件的所有点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,分别沿长方形纸片ABCD和正方形纸片EFGH的对角线AC,EG剪开,拼成如图2所示的ALMN,若中间空白部分四边形OPQR恰好是正方形,且ALMN的面积为50,则正方形EFGH的面积为( )
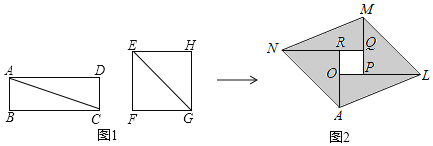
A. 24 B. 25 C. 26 D. 27
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小西“过直线外一点作这条直线的垂线”的尺规作图过程.
已知:直线l及直线l外一点P.
求作:直线PQ,使得PQ⊥l.
做法:如图,
①在直线l的异侧取一点K,以点P为圆心,PK长为半径画弧,交直线l于点A,B;
②分别以点A,B为圆心,大于![]() AB的同样长为半径画弧,两弧交于点Q(与P点不重合);
AB的同样长为半径画弧,两弧交于点Q(与P点不重合);
③作直线PQ,则直线PQ就是所求作的直线.
根据小西设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵PA= ,QA= ,
∴PQ⊥l( )(填推理的依据).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知点A(1,2),B(3,2),连接AB. 若对于平面内一点P,线段AB上都存在点Q,使得PQ≤1,则称点P是线段AB的“临近点”.
中,已知点A(1,2),B(3,2),连接AB. 若对于平面内一点P,线段AB上都存在点Q,使得PQ≤1,则称点P是线段AB的“临近点”.
(1)在点C(0,2),D(2,![]() ),E(4,1)中,线段AB的“临近点”是__________;
),E(4,1)中,线段AB的“临近点”是__________;
(2)若点M(m,n)在直线![]() 上,且是线段AB的“临近点”,求m的取值范围;
上,且是线段AB的“临近点”,求m的取值范围;
(3)若直线![]() 上存在线段AB的“临近点”,求b的取值范围.
上存在线段AB的“临近点”,求b的取值范围.
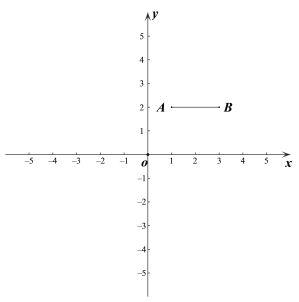
查看答案和解析>>
科目:初中数学 来源: 题型:
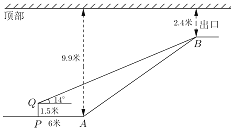
【题目】地铁10号线某站点出口横截面平面图如图所示,电梯![]() 的两端分别距顶部9.9米和2.4米,在距电梯起点
的两端分别距顶部9.9米和2.4米,在距电梯起点![]() 端6米的
端6米的![]() 处,用1.5米的测角仪测得电梯终端
处,用1.5米的测角仪测得电梯终端![]() 处的仰角为14°,求电梯
处的仰角为14°,求电梯![]() 的坡度与长度.(参考数据:
的坡度与长度.(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象如下所示,下列5个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() (
(![]() 的实数),其中正确的结论有几个?
的实数),其中正确的结论有几个?
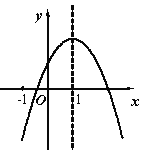
A. ①②③ B. ②③④ C. ②③⑤ D. ③④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com