
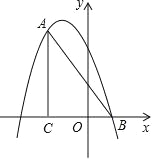
【题目】如图,在平面直角坐标系中,∠ACB=90°,OC=2BO,AC=6,点B的坐标为(1,0),抛物线y=﹣x2+bx+c经过A、B两点.
(1)求点A的坐标;
(2)求抛物线的解析式;
(3)点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE=![]() DE.
DE.
①求点P的坐标;
②在直线PD上是否存在点M,使△ABM为直角三角形?若存在,求出符合条件的所有点M的坐标;若不存在,请说明理由.
【答案】(1)y=﹣x2﹣3x+4;(2)①P(﹣1,6);②点M的坐标为:∴M(﹣1,3+![]() )或(﹣1,3﹣
)或(﹣1,3﹣![]() )或(﹣1,﹣1)或(﹣1,
)或(﹣1,﹣1)或(﹣1,![]() ).
).
【解析】
(1)先根据已知求点A的坐标,利用待定系数法求二次函数的解析式;
(2)①先得AB的解析式为:y=-2x+2,根据PD⊥x轴,设P(x,-x2-3x+4),则E(x,-2x+2),根据PE=![]() DE,列方程可得P的坐标;
DE,列方程可得P的坐标;
②先设点M的坐标,根据两点距离公式可得AB,AM,BM的长,分三种情况:△ABM为直角三角形时,分别以A、B、M为直角顶点时,利用勾股定理列方程可得点M的坐标.
(1)∵B(1,0),
∴OB=1,
∵OC=2OB=2,
∴C(﹣2,0),
Rt△ABC中,tan∠ABC=2,
∴![]() =2,
=2,
∴![]() =2,
=2,
∴AC=6,
∴A(﹣2,6),
把A(﹣2,6)和B(1,0)代入y=﹣x2+bx+c得:![]() ,
,
解得:![]() ,
,
∴抛物线的解析式为:y=﹣x2﹣3x+4;
(2)①∵A(﹣2,6),B(1,0),
易得AB的解析式为:y=﹣2x+2,
设P(x,﹣x2﹣3x+4),则E(x,﹣2x+2),
∵PE=![]() DE,
DE,
∴﹣x2﹣3x+4﹣(﹣2x+2)=![]() (﹣2x+2),
(﹣2x+2),
x=1(舍)或﹣1,
∴P(﹣1,6);
②∵M在直线PD上,且P(﹣1,6),
设M(﹣1,y),
∴AM2=(﹣1+2)2+(y﹣6)2=1+(y﹣6)2,
BM2=(1+1)2+y2=4+y2,
AB2=(1+2)2+62=45,
分三种情况:
i)当∠AMB=90°时,有AM2+BM2=AB2,
∴1+(y﹣6)2+4+y2=45,
解得:y=3![]() ,
,
∴M(﹣1,3+![]() )或(﹣1,3﹣
)或(﹣1,3﹣![]() );
);
ii)当∠ABM=90°时,有AB2+BM2=AM2,
∴45+4+y2=1+(y﹣6)2,y=﹣1,
∴M(﹣1,﹣1),
iii)当∠BAM=90°时,有AM2+AB2=BM2,
∴1+(y﹣6)2+45=4+y2,y=![]() ,
,
∴M(﹣1,![]() );
);
综上所述,点M的坐标为:∴M(﹣1,3+![]() )或(﹣1,3﹣
)或(﹣1,3﹣![]() )或(﹣1,﹣1)或(﹣1,
)或(﹣1,﹣1)或(﹣1,![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
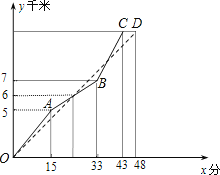
【题目】如图表示甲、乙两名选手在一次自行车越野赛中,路程y(千米)随时间x(分)变化的图象.下面几个结论:①比赛开始24分钟时,两人第一次相遇.②这次比赛全程是10千米.③比赛开始38分钟时,两人第二次相遇.正确的结论为_____(只填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形ABCD中,AB=BC,AD2+CD2=2AB2,CD⊥AD.

(1)求证:AB⊥BC.
(2)若AB=3CD,AD=17,求四边形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,菱形OABC的顶点A在x轴的正半轴上,顶点C的坐标为(1,![]() ).
).
(1)求图象过点B的反比例函数的解析式;
(2)求图象过点A,B的一次函数的解析式;
(3)在第一象限内,当以上所求一次函数的图象在所求反比例函数的图象下方时,请直接写出自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为打赢“脱贫攻坚”战,某地党委、政府联合某企业带领农户脱贫致富,该企业给某低收入户发放如图①所示的长方形和正方形纸板,供其加工做成如图②所示的A,B两款长方体包装盒(其中A款包装盒无盖,B款包装盒有盖).请你帮这户人家计算他家领取的360张长方形纸板和140张正方形纸板,做成A,B型盒子分别多少个能使纸板刚好全部用完?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于国家对农业的大力扶持,农民的种粮积极性得到极大提高.国家统计局提供的数据表明,我国粮食产量连续两年大幅增长,![]() 年粮食产量为
年粮食产量为![]() 亿斤,
亿斤,![]() 年达到了
年达到了![]() 亿斤,若要求这两年粮食产量的平均增长率,可设平均增长率为
亿斤,若要求这两年粮食产量的平均增长率,可设平均增长率为![]() ,列方程为________.
,列方程为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣2,3)、B(4,3)、C(﹣1,﹣3).
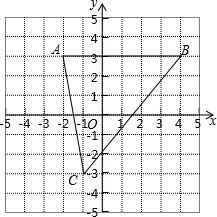
(1)求点C到x轴的距离;
(2)分别求△ABC的三边长;
(3)点P在y轴上,当△ABP的面积为6时,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
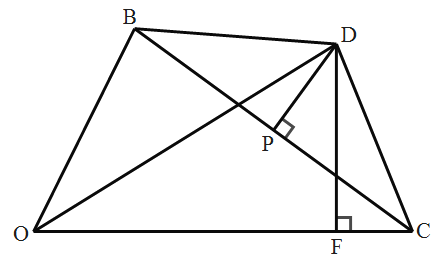
【题目】如图,在△OBC中,边BC的垂直平分线交∠BOC的平分线于点D,连接DB,DC,过点D作DF⊥OC于点F.
(1)若∠BOC=60°,求∠BDC的度数;
(2)若∠BOC=![]() ,则∠BDC= ;(直接写出结果)
,则∠BDC= ;(直接写出结果)
(3)直接写出OB,OC,OF之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】六一期间,某公园游戏场举行“迎奥运”活动.有一种游戏的规则是:在一个装有![]() 个红球和若干个白球(每个球除颜色外其他相同)的袋中,随机摸一个球,摸到一个红球就得到一个奥运福娃玩具.已知参加这种游戏活动为
个红球和若干个白球(每个球除颜色外其他相同)的袋中,随机摸一个球,摸到一个红球就得到一个奥运福娃玩具.已知参加这种游戏活动为![]() 人次,公园游戏场发放的福娃玩具为
人次,公园游戏场发放的福娃玩具为![]() 个.
个.
![]() 求参加一次这种游戏活动得到福娃玩具的概率;
求参加一次这种游戏活动得到福娃玩具的概率;
![]() 请你估计袋中白球接近多少个?
请你估计袋中白球接近多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com