
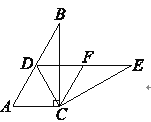
【题目】如图,在△OBC中,边BC的垂直平分线交∠BOC的平分线于点D,连接DB,DC,过点D作DF⊥OC于点F.
(1)若∠BOC=60°,求∠BDC的度数;
(2)若∠BOC=![]() ,则∠BDC= ;(直接写出结果)
,则∠BDC= ;(直接写出结果)
(3)直接写出OB,OC,OF之间的数量关系.
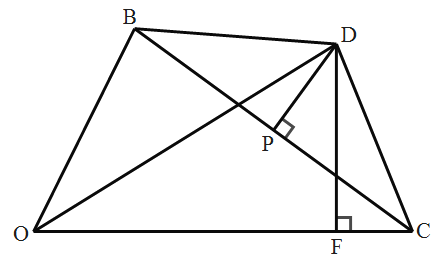
【答案】(1)120°;(2)180°-α;(3)OB+OC=2OF
【解析】
(1)首先过点D作DE⊥OB于E,易证得△DEB≌△DFC(HL),即可得∠BDC=∠EDF,又由∠EOF+∠EDF=180゜,即可求得答案;
(2)由(1),可求得∠BDC的度数;
(3) OB+OC=OE+OF=2OF
解:(1)过点D作DE⊥OB,交OB延长线于点E,DF⊥OC于F,
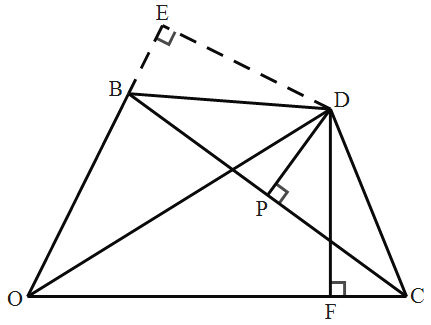
∵OD是∠BOC的平分线,
∴DE=DF,
∵DP是BC的垂直平分线,
∴BD=CD,
在Rt△DEB和Rt△DFC中,![]()
∴△DEB≌△DFC(HL)
∴∠BDE=∠CDF,
∴∠BDC=∠EDF,
∵∠EOF+∠EDF=180゜,
∵∠BOC=60゜,
∴∠BDC=∠EDF=120゜.
(2)∵∠EOF+∠EDF=180゜,
∵∠BOC=α,
∴∠BDC=∠EDF=180゜-α.
故答案为:180゜-α.
(3)由(1)知OB+OC=OE+OF=2OF


科目:初中数学 来源: 题型:
【题目】某班男同学身高情况如下表,则其中数据167cm( )
身高(cm) | 170 | 169 | 168 | 167 | 166 | 165 | 164 | 163 |
人数(人) | 1 | 2 | 5 | 8 | 6 | 3 | 3 | 2 |
A.是平均数B.是众数但不是中位数.
C.是中位数但不是众数D.是众数也是中位数
查看答案和解析>>
科目:初中数学 来源: 题型:
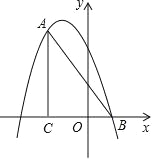
【题目】如图,在平面直角坐标系中,∠ACB=90°,OC=2BO,AC=6,点B的坐标为(1,0),抛物线y=﹣x2+bx+c经过A、B两点.
(1)求点A的坐标;
(2)求抛物线的解析式;
(3)点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE=![]() DE.
DE.
①求点P的坐标;
②在直线PD上是否存在点M,使△ABM为直角三角形?若存在,求出符合条件的所有点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在解决问题:已知a=![]() ,求2a2-8a+1的值,他是这样分析与解答的:
,求2a2-8a+1的值,他是这样分析与解答的:
因为a=![]() =
=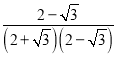 =2-
=2-![]() ,
,
所以a-2=-![]() .
.
所以(a-2)2=3,即a2-4a+4=3.
所以a2-4a=-1.
所以2a2-8a+1=2(a2-4a)+1=2×(-1)+1=-1.
请你根据小明的分析过程,解决如下问题:
(1)计算: ![]() = - .
= - .
(2)计算:![]() +…+
+…+![]() ;
;
(3)若a=![]() ,求4a2-8a+1的值.
,求4a2-8a+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转,可以得到△DEC.若点D刚好落在AB边上,取DE边的中点F,连接FC,试判断四边形ACFD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合).在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)求证:△AEF是等腰直角三角形;
(2)如图2,将△CED绕点C逆时针旋转,当点E在线段BC上时,连接AE,求证:AF=![]() AE;
AE;
(3)如图3,将△CED绕点C继续逆时针旋转,当平行四边形ABFD为菱形,且△CED在△ABC的下方时,若AB=2![]() ,CE=2,求线段AE的长.
,CE=2,求线段AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边三角形ABC,点D为线段BC上一点,以线段DB为边向右侧作△DEB,使DE=CD,若∠ADB=m°,∠BDE=(180﹣2m)°,则∠DBE的度数是( )

A.(m﹣60)°B.(180﹣2m)°C.(2m﹣90)°D.(120﹣m)°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC边上的一点,AB=DB,BE平分∠ABC,交AC边于点E,连接DE.

(1)求证:AE=DE;
(2)若∠A=100°,∠C=50°,求∠AEB的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com