
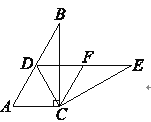
【题目】如图所示,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转,可以得到△DEC.若点D刚好落在AB边上,取DE边的中点F,连接FC,试判断四边形ACFD的形状,并说明理由.
【答案】见解析.
【解析】
由在Rt△ABC 中,∠ACB=90°,∠B=30°,易得△ACD是等边三角形,则可得AC=AD=![]() AB,又由旋转的性质与直角三角形斜边的中线的性质,证得DF=CF=
AB,又由旋转的性质与直角三角形斜边的中线的性质,证得DF=CF=![]() DE,则可得AC=CF=DF=AD,继而证得四边形ACFD是菱形.
DE,则可得AC=CF=DF=AD,继而证得四边形ACFD是菱形.
解:四边形ACFD是菱形.
理由如下:
∵在Rt△ABC中,∠ACB=90°,∠B=30°,
∴∠A=90°-∠B=60°,AC=![]() AB.
AB.
∵将△ABC绕点C按顺时针方向旋转,得到△DEC,
∴CA=CD,AB=DE,∠ACB=∠DCE=90°,
∴△ACD是等边三角形,∴AC=AD.
∵F是DE的中点,∴DF=CF=![]() DE.
DE.
∴AC=CF=DF=AD,
∴四边形ACFD是菱形.


 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】从边长为a的大正方形纸板中挖去一个边长为b的小正方形后,将其裁成四个相同的等腰梯形(如图1),然后拼成一个平行四边形(如图2)。那么通过计算两个图形的阴影部分的面积,可以验证成立的公式是( )
A.a2-b2=(a-b)2 | B.(a+b)2="a+2ab+b" |
C.(a-b)2=a2-2ab+b2 | D.a2-b2=(a-b)(a+b) |

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为打赢“脱贫攻坚”战,某地党委、政府联合某企业带领农户脱贫致富,该企业给某低收入户发放如图①所示的长方形和正方形纸板,供其加工做成如图②所示的A,B两款长方体包装盒(其中A款包装盒无盖,B款包装盒有盖).请你帮这户人家计算他家领取的360张长方形纸板和140张正方形纸板,做成A,B型盒子分别多少个能使纸板刚好全部用完?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣2,3)、B(4,3)、C(﹣1,﹣3).
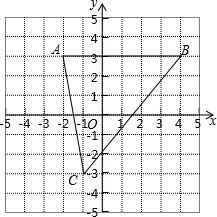
(1)求点C到x轴的距离;
(2)分别求△ABC的三边长;
(3)点P在y轴上,当△ABP的面积为6时,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,抛物线y=-x2+2![]() x的顶点为A点,且与x轴的正半轴交于点B,P点为该抛物线对称轴上一点,则OP+
x的顶点为A点,且与x轴的正半轴交于点B,P点为该抛物线对称轴上一点,则OP+![]() AP的最小值为( ).
AP的最小值为( ).
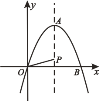
A. 3 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
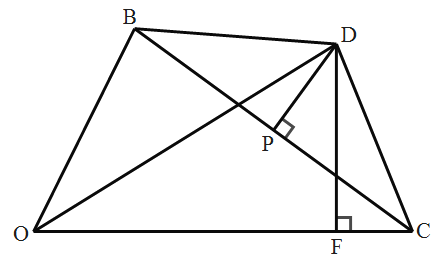
【题目】如图,在△OBC中,边BC的垂直平分线交∠BOC的平分线于点D,连接DB,DC,过点D作DF⊥OC于点F.
(1)若∠BOC=60°,求∠BDC的度数;
(2)若∠BOC=![]() ,则∠BDC= ;(直接写出结果)
,则∠BDC= ;(直接写出结果)
(3)直接写出OB,OC,OF之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
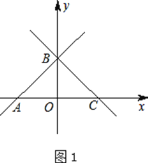
【题目】如图1,在平面直角坐标系![]() 中,直线AB与
中,直线AB与![]() 轴交于点A、与
轴交于点A、与![]() 轴交于点B,且∠ABO=45°,A(-6,0),直线BC与直线AB关于
轴交于点B,且∠ABO=45°,A(-6,0),直线BC与直线AB关于![]() 轴对称.
轴对称.
(1)求△ABC的面积;
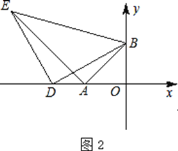
(2)如图2,D为OA延长线上一动点,以BD为直角边,D为直角顶点,作等腰直角△BDE,求证:AB⊥AE;
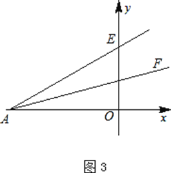
(3)如图3,点E是![]() 轴正半轴上一点,且∠OAE=30°,AF平分∠OAE,点M是射线AF上一动点,点N是线段AO上一动点,判断是否存在这样的点M,N,使OM+NM的值最小?若存在,请写出其最小值,并加以说明.
轴正半轴上一点,且∠OAE=30°,AF平分∠OAE,点M是射线AF上一动点,点N是线段AO上一动点,判断是否存在这样的点M,N,使OM+NM的值最小?若存在,请写出其最小值,并加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
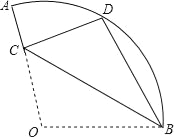
【题目】已知:如图,在扇形OAB中,∠AOB=110°,半径OA=18,将扇形OAB沿过点B的直线折叠,点O恰好落在弧AB上的点D处,折痕交OA于点C,则弧AD的长为( )
A. 2π B. 3π C. 4π D. 5π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com