
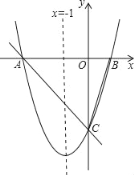
【题目】如图,对称轴为直线x=﹣1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A,B两点.
(1)若点A的坐标为(﹣4,0),求点B的坐标.
(2)若已知a=1,点A的坐标为(﹣3,0),C为抛物线与y轴的交点.
①若点P在抛物线上,且S△POC=4S△BOC,求点P的坐标;
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.
【答案】(1)B(2,0);(2)①P(4,21),(﹣4,5);②当m=﹣![]() 时,QD的最大值为
时,QD的最大值为![]() .
.
【解析】
(1)根据抛物线与x轴的两个交点关于对称轴对称,可求B点坐标;
(2)①根据题意可求抛物线解析式,可求△BOC的面积,根据S△POC=4S△BOC,可求P点坐标;
③求出直线AC解析式,设点Q(m,-m-3)(-3≤m≤0),则点D(m,m2+2m-3),根据二次函数的最值求法,可求QD的最大值.
(1)∵对称轴是直线x=﹣1,点A的坐标为(﹣4,0),且A,B关于对称轴对称,
∴B(2,0);
(2)①∵对称轴是直线x=﹣1,点A的坐标为(﹣3,0),且A,B关于对称轴对称,
∴B(1,0),即OB=1,
∵a=1,
∴抛物线解析式y=(x﹣1)(x+3)=x2+2x﹣3;
当x=0时,y=﹣3,
∴点C(0,﹣3),即OC=3,
∴S△BOC=![]() OB×OC=
OB×OC=![]() ,
,
设P(x,x2+2x﹣3),
∴S△POC=![]() ×3×|x|,
×3×|x|,
∵S△POC=4S△BOC,
∴![]() |x|=4×
|x|=4×![]() ,
,
∴x=±4,
∴P(4,21),(﹣4,5);
②∵点A(﹣3,0),点C(0,﹣3),
∴直线AC解析式y=﹣x﹣3,
∴设点Q(m,﹣m﹣3)(﹣3≤m≤0),
则点D(m,m2+2m﹣3),
∴QD=﹣m﹣3﹣(m2+2m﹣3)=﹣(m+![]() )2+
)2+![]() ,
,
∴当m=﹣![]() 时,QD的最大值为
时,QD的最大值为![]() .
.


科目:初中数学 来源: 题型:
【题目】阅读下面的情景对话,然后解答问题:
老师:我们新定义一种三角形,两边平方和等于第三边平方的2倍的三角形叫做奇异三角形.
小华:等边三角形一定是奇异三角形!
小明:那直角三角形是否存在奇异三角形呢?
(1)根据“奇异三角形”的定义,请你判断小华提出的命题:“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt△ABC中,AB=c,AC=b,BC=a,且c>b>a,若Rt△ABC是奇异三角形,求a:b:c;
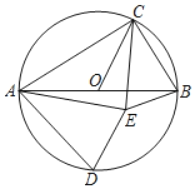
(3)如图,AB是⊙O的直径,C是⊙O上一点(不与点A、B重合),D是半圆![]() 中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
①求证:△ACE是奇异三角形:
②当△ACE是直角三角形时,求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】细心的小明发现,一元二次方程ax2+bx+c=0(a≠0)根与系数之间的“秘密”关系.
(1)当x=1时有a+b+c=0,当x=﹣1时有a﹣b+c=0.若9a+c=3b,求x;
(2)若2a+b=0,3a+c=0,写出满足条件的一个一元二次方程,并求另一个根;
(3)当老师写出方程2x2﹣3x﹣1=0,要求不解方程判断根的情况时,小明立即回答,有两个不相等的实数根.据此,你能根据一元二次方程系数a、b、c的符号以及相互之间的数量关系,写出一些关于一元二次方程ax2+bx+c=0(a≠0)根与系数之间的规律吗?请写一写(至少两条).
查看答案和解析>>
科目:初中数学 来源: 题型:
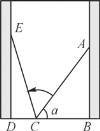
【题目】如图,小巷左右两侧是竖直的墙,一架梯子AC斜靠在右墙,测得梯子顶端距离地面AB=2米,梯子与地面夹角α的正弦值sinα=0.8.梯子底端位置不动,将梯子斜靠在左墙时,顶端距离地面2.4米,则小巷的宽度为( )
A. 0.7米B. 1.5米
C. 2.2米D. 2.4米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班准备选一名学生参加数学史知识竞赛,现统计了两名选手本学期的五次测试 成绩:甲:83,80,90,87, 85; 乙:78,92,82,89,84.
(1)请根据上面的数据完成下表:
极差 | 平均数 | 方差 | |
甲 | 10 | ________ | ________ |
乙 | _________ | 85 | 24.8 |
(2)请你推选出一名参赛选手,并用所学的统计知识说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
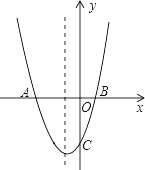
【题目】如图,已知:二次函数y=x2+bx+c 的图象与x轴交于A,B两点,其中A点坐标为(-3,0),与 y 轴交于点 C(0,-3)在抛物线上.
(1)求抛物线的表达式;
(2)抛物线的对称轴上有一动点 P,求出当 PB+PC 最小时点 P的坐标;
(3)若抛物线上有一动点Q,使△ABQ的面积为6,求Q点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
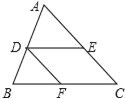
【题目】如图,在△ABC中,点D、E、F分别在边AB、AC、BC上,DE∥BC,DF∥AC,若△ADE与四边形DBCE的面积相等,则△DBF与△ADE的面积之比为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 3-2
D. 3-2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件50元.当售价为每件70元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元、每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com