【题目】某班准备选一名学生参加数学史知识竞赛，现统计了两名选手本学期的五次测试 成绩：甲：83，80，90，87， 85； 乙：78，92，82，89，84．
（1）请根据上面的数据完成下表：
极差 | 平均数 | 方差 | |
甲 | 10 | ________ | ________ |
乙 | _________ | 85 | 24.8 |
（2）请你推选出一名参赛选手，并用所学的统计知识说明理由.
备战中考寒假系列答案科目：初中数学 来源： 题型：
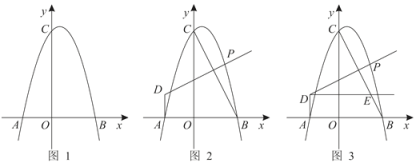
【题目】已知：如图，抛物线
交x轴于A（－2，0），B（3，0）两点，交y轴于点C（0，6）．
（1）写出a，b，c的值；
（2）连接BC，点P为第一象限抛物线上一点，过点A作AD⊥x轴，过点P作PD⊥BC于交直线AD于点D，设点P的横坐标为t，AD长为h．
①求h与t的函数关系式和h的最大值（请求出自变量t的取值范围）；
②过第二象限点D作DE∥AB交BC于点E，若DP=CE，时，求点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
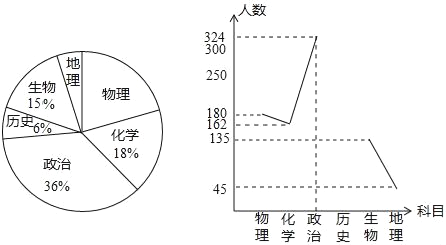
【题目】某校对九年级学生进行随机抽样调查，被抽到的学生从物理、化学、生物、地理、历史和政治这六科中选出自己最喜欢的科目，将调查数据汇总整理后，绘制了两幅不同的统计图，请你根据图中信息解答下列问题：
（1）被抽查的学生共有多少人？求出地理学科所在扇形的圆心角；
（2）将折线统计图补充完整；
（3）若该校九年级学生约2000人请你估算喜欢物理学科的人数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC是等边三角形，CE是外角平分线，点D在AC上，连结BD并延长与CE交于点E．
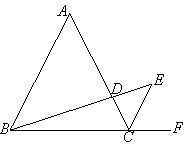
（1）求证：△ABD∽△CED．
（2）若AB＝6，AD＝2CD，求BE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，∠ACB＝90°，sinA＝
，BC＝8，点D是AB的中点，过点B作CD的垂线，垂足为点E.
(1)求线段CD的长；
(2)求cos∠ABE的值。
查看答案和解析>>
科目：初中数学 来源： 题型：
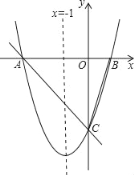
【题目】如图，对称轴为直线x＝﹣1的抛物线y＝ax2+bx+c（a≠0）与x轴相交于A，B两点．
（1）若点A的坐标为（﹣4，0），求点B的坐标．
（2）若已知a＝1，点A的坐标为（﹣3，0），C为抛物线与y轴的交点．
①若点P在抛物线上，且S△POC＝4S△BOC，求点P的坐标；
②设点Q是线段AC上的动点，作QD⊥x轴交抛物线于点D，求线段QD长度的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商店销售一种成本为20元的商品，经调研，当该商品每件售价为30元时，每天可销售200件：当每件的售价每增加1元，每天的销量将减少5件．
求销量
件
与售价
元之间的函数表达式；
如果每天的销量不低于150件，那么，当售价为多少元时，每天获取的利润最大，最大利润是多少？
该商店老板热心公益事业，决定从每天的销售利润中捐出100元给希望工程，为保证捐款后每天剩余利润不低于2900元，请直接写出该商品售价的范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们定义：有一组邻角相等的凸四边形叫做“等邻角四边形”．
概念理解：在“矩形、菱形和正方形”这三种特殊四边形中，不一定是“等邻角四边形”的是______．
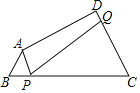
问题探究：如图，在等邻角四边形ABCD中，∠B=∠C，AB=3，BC=9，P为线段BC上一动点（不包含端点B，C），Q为直线CD上一动点，连结PA，PQ，在P，Q的运动过程中始终满足∠APQ=∠B，当CQ达到最大时，试求此时BP的长．
应用拓展：在以60°为等角的等邻角四边形ABCD中，∠D=90°，若AB=3，AD=
，试求等邻角四边形ABCD的周长．
查看答案和解析>>
科目：初中数学 来源： 题型：
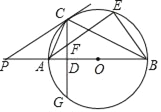
【题目】如图，AB为⊙O的直径，P是BA延长线上一点，CG是⊙O的弦∠PCA＝∠ABC，CG⊥AB，垂足为D
（1）求证：PC是⊙O的切线；
（2）求证：
；
（3）过点A作AE∥PC交⊙O于点E，交CD于点F，连接BE，若sin∠P＝
，CF＝5，求BE的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
