
【题目】如图,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,
,![]() 为
为![]() 上一点,经过点
上一点,经过点![]() ,
,![]() 的
的![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
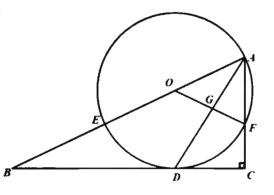
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)设![]() ,
,![]() ,试用含
,试用含![]() 的代数式表示线段
的代数式表示线段![]() 的长;
的长;
(3)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】(1)连接OD,由AD为角平分线得到一对角相等,再由等边对等角得到一对角相等,等量代换得到内错角相等,进而得到OD与AC平行,得到OD与BC垂直,即可得证;
(2)连接DF,由(1)得到BC为圆O的切线,由弦切角等于夹弧所对的圆周角,进而得到三角形ABD与三角形ADF相似,由相似得比例,即可表示出AD;
(3)连接EF,设圆的半径为r,由sinB的值,利用锐角三角函数定义求出r的值,由直径所对的圆周角为直角,得到EF与BC平行,得到sin∠AEF=sinB,进而求出DG的长即可.
(1)证明:如图,连接OD,
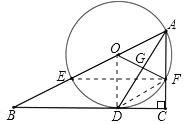
∵AD为∠BAC的角平分线,
∴∠BAD=∠CAD,
∵OA=OD,
∴∠ODA=∠OAD,
∴∠ODA=∠CAD,
∴OD∥AC,
∵∠C=90°,
∴∠ODC=90°,
∴OD⊥BC,
∴BC为圆O的切线;
(2)连接DF,由(1)知BC为圆O的切线,
∴∠FDC=∠DAF,
∴∠CDA=∠CFD,
∴∠AFD=∠ADB,
∵∠BAD=∠DAF,
∴△ABD∽△ADF,
∴![]()
,即AD2=ABAF=xy,
则AD=![]()
(3)连接EF,在Rt△BOD中,sinB=![]() ,
,
设圆的半径为r,可得![]() ,
,
解得:r=5,
∴AE=10,AB=18,
∵AE是直径,
∴∠AFE=∠C=90°,
∴EF∥BC,
∴∠AEF=∠B,
∴sin∠AEF=![]() ,
,
∴AF=AEsin∠AEF=10×![]() ,
,
∵AF∥OD,
∴![]() ,即DG=
,即DG=![]() AD,
AD,
∵AD=![]() ,
,
则DG=![]() ×
×![]() =
=![]() .
.


科目:初中数学 来源: 题型:
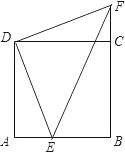
【题目】已知:如图,E点是正方形ABCD的边AB上一点,AB=4,DE=6,△DAE逆时针旋转后能够与△DCF重合.
(1)旋转中心是 .旋转角为 度.
(2)请你判断△DFE的形状,并说明理由.
(3)求四边形DEBF的周长和面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.
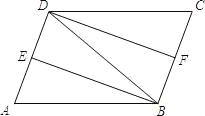
(1)求证:△ABE≌△CDF;
(2)若AB=DB,求证:四边形DFBE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 是定长线段
是定长线段![]() 上一定点.点
上一定点.点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 上,
上,![]() 、
、![]() 两点分别从
两点分别从![]() 、
、![]() 出发,分别以
出发,分别以![]() /
/![]() 、
、![]() /
/![]() 的速度沿直线
的速度沿直线![]() 同时向左运动.
同时向左运动.
(1)若![]() ,当点
,当点![]() 、
、![]() 运动了
运动了![]() ,求
,求![]() 的值;
的值;
(2)若点![]() 、
、![]() 运动时,总有
运动时,总有![]() ,则
,则![]() _____
_____![]() ;
;
(3)在(2)的条件下,点![]() 是直线
是直线![]() 上一点,且
上一点,且![]() ,求
,求![]() 的值.
的值.
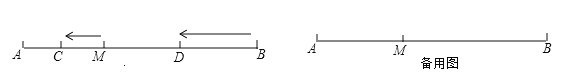
查看答案和解析>>
科目:初中数学 来源: 题型:
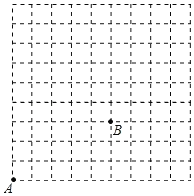
【题目】如图,在9×9的方格(每小格边长为1个单位)中,有格点A,B现点A沿网格线跳动规定:向右跳动一格需要m秒,向上跳动一格需要n秒,且每次跳动后均落在格点上.
(1)点A跳到点B,需要 秒(用含m,n的代数式表示).
(2)已知m=1,n=2.
①若点A向右跳动3秒,向上跳动10秒到达点C,请在图中标出点C的位置,并求出以BC为边的正方形的面积.
②若点A跳动5秒到达点D,请直接写出点D与点B之间距离的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着移动互联网的快速发展,基于互联网的共享单车应运而生.为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9.
(1)这组数据的中位数是 ,众数是 ;
(2)计算这10位居民一周内使用共享单车的平均次数;
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果mx+n=0,其中m、n为有理数,x为无理数,那么m=0且n=0.
(1)如果![]() ,其中a、b为有理数,那么a= ,b= .
,其中a、b为有理数,那么a= ,b= .
(2)如果![]() ,其中a、b为有理数,求a+2b的值.
,其中a、b为有理数,求a+2b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,△ADE的顶点D,E分别在BC,AC上,且∠DAE=90°,AD=AE.若∠C+∠BAC=145°,则∠EDC的度数为( )

A. 17.5° B. 12.5° C. 12° D. 10°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com