
【题目】已知:如图,E点是正方形ABCD的边AB上一点,AB=4,DE=6,△DAE逆时针旋转后能够与△DCF重合.
(1)旋转中心是 .旋转角为 度.
(2)请你判断△DFE的形状,并说明理由.
(3)求四边形DEBF的周长和面积.
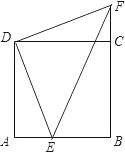
【答案】(1)D,90;(2) △DFE的形状是等腰直角三角形,见解析;(3)20,16
【解析】
(1)由题意可知要确定旋转中心及旋转的角度,首先确定哪是对应点,即可确定旋转中心以及旋转角;
(2)根据旋转的性质,可以得到旋转前后的两个图形全等,以及旋转角的定义即可作出判断;
(3)由题意根据△DAE≌△DCF,可以得到:AE=CF,DE=DF,则四边形DEBF的周长就是正方形的三边的和与DE的和.
解:(1)由题意可知旋转中心是点D,
![]() 即为旋转角为90度.
即为旋转角为90度.
(2)根据旋转的性质可得:△DAE≌△DCF,则DE=DF,∠EDF=∠ADC=90°,
则△DFE的形状是等腰直角三角形.
(3)四边形DEBF的周长是BE+BC+CF+DF+DE=AB+BC+DE+DF=4+4+6+6=20;
由题意可知四边形DEBF的面积等于正方形ABCD的面积=16.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】一家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元,若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:
(1)甲,乙两组工作一天,商店各应付多少钱?
(2)已知甲单独完成需12天,乙单独完成需24天,单独请哪个组,商店所需费用最少?
(3)若装修完后,商店每天可贏利200元,你认为如何安排施工更有利于商店?请你帮助商店决策.(可用(1)(2)问的条件及结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组织340名师生进行长途考察活动,带有行李170件,计划租用甲、乙两种型号的汽车共10辆.经了解,甲车每辆最多能载40人和16件行李,乙车每辆最多能载30人和20件行李.
(1)请你帮助学校设计所有可行的租车方案.
(2)如果甲车的租金为每辆2 000元,乙车的租金为每辆1 800元,问哪种可行方案使租车费用最省?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,我们把对角线互相垂直的四边形叫做垂美四边形.

(l)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由.
(2)性质探宄:试探索垂美四边形ABCD两组对边AB,CD与BC,AD之间的数量关系.
猜想结论:(要求用文字语言叙述)
写出证明过程(先画出图形,写出已知、求证)
(3)问题解决:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5,求GE长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科技改变世界.2017年底,快递分拣机器人从微博火到了朋友圈.据介绍,这些机器人不仅可以自动规划最优路线,将包裹准确地放入相应的路口,还会感应避让障碍物,自动归队取包裹,没电的时候还会自己找充电桩充电.某快递公司启用40台A种机器人、150台B种机器人分拣快递包裹,A、B两种机器人全部投入工作,1小时共可以分拣0.77万件包裹;若全部A种机器人工作1.5小时,全部B种机器人工作2小时,一共可以分拣1.38万件包裹.
(1)求两种机器人每台每小时各分拣多少件包裹?
(2)为进一步提高效率,快递公司计划再购进A、B两种机器人共100台.若要保证新购进的这批机器人每小时的总分拣量不少于5500件,求至少应购进A种机器人多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着粤港澳大湾区建设的加速推进,广东省正加速布局以5G等为代表的战略性新兴产业,据统计,目前广东5G基站的数量约1.5万座,计划到2020年底,全省5G基站数是目前的4倍,到2022年底,全省5G基站数量将达到17.34万座。
(1)计划到2020年底,全省5G基站的数量是多少万座?;
(2)按照计划,求2020年底到2022年底,全省5G基站数量的年平均增长率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求完成下列证明:
已知:如图,AB∥CD,直线AE交CD于点C,∠BAC+∠CDF=180°.

求证:AE∥DF.
证明: ∵AB∥CD(____________________________) ,
∴∠BAC=∠DCE(__________________________________________________________________________).
∵∠BAC+∠CDF=180°(已知),
∴____________ +∠CDF=180°(____________________________________).
∴AE∥DF(______________________________________________________________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() ABCD中,∠ADC的平分线交直线BC于点E、交AB的延长线于点F,连接AC.
ABCD中,∠ADC的平分线交直线BC于点E、交AB的延长线于点F,连接AC.
(1)如图1,若∠ADC=90°,G是EF的中点,连接AG、CG.
①求证:BE=BF;
②请判断△AGC的形状,并说明理由.
(2)如图2,若∠ADC=60°,将线段FB绕点F顺时针旋转60°至FG,连接AG、CG,判断△AGC的形状.(直接写出结论不必证明)
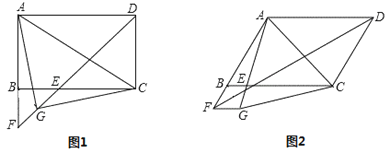
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,
,![]() 为
为![]() 上一点,经过点
上一点,经过点![]() ,
,![]() 的
的![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
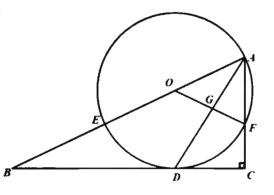
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)设![]() ,
,![]() ,试用含
,试用含![]() 的代数式表示线段
的代数式表示线段![]() 的长;
的长;
(3)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com