
【题目】科技改变世界.2017年底,快递分拣机器人从微博火到了朋友圈.据介绍,这些机器人不仅可以自动规划最优路线,将包裹准确地放入相应的路口,还会感应避让障碍物,自动归队取包裹,没电的时候还会自己找充电桩充电.某快递公司启用40台A种机器人、150台B种机器人分拣快递包裹,A、B两种机器人全部投入工作,1小时共可以分拣0.77万件包裹;若全部A种机器人工作1.5小时,全部B种机器人工作2小时,一共可以分拣1.38万件包裹.
(1)求两种机器人每台每小时各分拣多少件包裹?
(2)为进一步提高效率,快递公司计划再购进A、B两种机器人共100台.若要保证新购进的这批机器人每小时的总分拣量不少于5500件,求至少应购进A种机器人多少台?
【答案】(1)A种机器人每台每小时分拣80件包裹,B种机器人每台每小时分拣30件包裹;(2)至少应购进A种机器人50台
【解析】
(1)由题意可知A种机器人每台每小时分拣x件包裹,B种机器人每台每小时分拣y件包裹,根据题意列方程组即可得到结论;
(2)根据题意设应购进A种机器人a台,购进B种机器人(100﹣a)台,由题意得出不等式,进行求解即可得到结论.
解:(1)A种机器人每台每小时拣x件包裹,B种机器人每台每小时分拣y件包裹,
由题意得![]() ,
,
解得![]() ,
,
答:A种机器人每台每小时分拣80件包裹,B种机器人每台每小时分拣30件包裹;
(2)设应购进A种机器人a台,购进B种机器人(100﹣a)台,
由题意得,80a+30(100﹣a)≥5500,
解得:a≥50,
答:至少应购进A种机器人50台.


科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径为2,AB为直径,CD为弦.AB与CD交于点M,将 ![]() 沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC
沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC
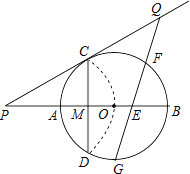
(1)求CD的长;
(2)求证:PC是⊙O的切线;
(3)点G为 ![]() 的中点,在PC延长线上有一动点Q,连接QG交AB于点E.交
的中点,在PC延长线上有一动点Q,连接QG交AB于点E.交 ![]() 于点F(F与B、C不重合).问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由.
于点F(F与B、C不重合).问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016浙江省衢州市)如图,正方形ABCD的顶点A,B在函数![]() (x>0)的图象上,点C,D分别在x轴,y轴的正半轴上,当k的值改变时,正方形ABCD的大小也随之改变.
(x>0)的图象上,点C,D分别在x轴,y轴的正半轴上,当k的值改变时,正方形ABCD的大小也随之改变.
(1)当k=2时,正方形A′B′C′D′的边长等于____.
(2)当变化的正方形ABCD与(1)中的正方形A′B′C′D′有重叠部分时,k的取值范围是______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小靓用七巧板拼成一幅装饰图,放入长方形ABCD内,装饰图中的三角形顶点E,F分别在边AB,BC上,三角形①的边GD在边AD上,若图1正方形中MN=1,则CD=____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣2x2+8x﹣6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )

A. ﹣2<m<![]() B. ﹣3<m<﹣
B. ﹣3<m<﹣![]() C. ﹣3<m<﹣2 D. ﹣3<m<﹣
C. ﹣3<m<﹣2 D. ﹣3<m<﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,E点是正方形ABCD的边AB上一点,AB=4,DE=6,△DAE逆时针旋转后能够与△DCF重合.
(1)旋转中心是 .旋转角为 度.
(2)请你判断△DFE的形状,并说明理由.
(3)求四边形DEBF的周长和面积.
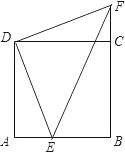
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,P1、P2是反比例函数y=![]() (k>0)在第一象限图象上的两点,点A1的坐标为(4,0).若△P1OA1与△P2A1A2均为等腰直角三角形,其中点P1、P2为直角顶点.
(k>0)在第一象限图象上的两点,点A1的坐标为(4,0).若△P1OA1与△P2A1A2均为等腰直角三角形,其中点P1、P2为直角顶点.
(1)直接写出反比例函数的解析式.
(2)①求P2的坐标.
②根据图象直接写出在第一象限内,当x满足什么条件时,经过点P1、P2的一次函数的函数值大于反比例函数y=![]() 的函数值.
的函数值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P,且AE=CF.
(1)求证:AF=BE,并求∠FPB的度数;
(2)若AE=2,试求AP·AF的值.
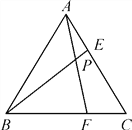
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com