
【题目】(2016浙江省衢州市)如图,正方形ABCD的顶点A,B在函数![]() (x>0)的图象上,点C,D分别在x轴,y轴的正半轴上,当k的值改变时,正方形ABCD的大小也随之改变.
(x>0)的图象上,点C,D分别在x轴,y轴的正半轴上,当k的值改变时,正方形ABCD的大小也随之改变.
(1)当k=2时,正方形A′B′C′D′的边长等于____.
(2)当变化的正方形ABCD与(1)中的正方形A′B′C′D′有重叠部分时,k的取值范围是______________.

【答案】 ![]()
![]() ≤k≤18.
≤k≤18.
【解析】解:(1)如图,过点A′作AE⊥y轴于点E,过点B′⊥x轴于点F,则∠A′ED′=90°.
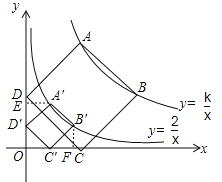
∵四边形A′B′C′D′为正方形,∴A′D′=D′C′,∠A′D′C′=90°,∴∠OD′C′+∠ED′A′=90°.∵∠OD′C′+∠OC′D′=90°,∴∠ED′A′=∠OC′D′.
在△A′ED′和△D′OC′中,∵∠ED′A′=∠OC′D′,∠A′ED′=∠D′OC′,A′D′=D′C′,∴△A′ED′≌△D′OC′(AAS),∴OD′=EA′,OC′=ED′.
同理△B′FC′≌△C′OD′.
设OD′=a,OC′=b,则EA′=FC′=OD′=a,ED′=FB′=OC′=b,即点A′(a,a+b),点B′(a+b,b).∵点A′、B′在反比例函数![]() 的图象上,∴
的图象上,∴![]() ,解得:
,解得:![]() 或
或![]() (舍去).
(舍去).
在Rt△C′OD′中,∠C′OD′=90°,OD′=OC′=1,∴C′D′=![]() =
=![]() .
.
故答案为:![]() .
.
(2)设直线A′B′解析式为![]() ,直线C′D′解析式为
,直线C′D′解析式为![]() ,∵点A′(1,2),点B′(2,1),点C′(1,0),点D′(0,1),∴有
,∵点A′(1,2),点B′(2,1),点C′(1,0),点D′(0,1),∴有![]() 和
和![]() ,解得:
,解得:![]() 和
和![]() ,∴直线A′B′解析式为y=﹣x+3,直线C′D′解析式为y=﹣x+1.设点A的坐标为(m,2m),点D坐标为(0,n).
,∴直线A′B′解析式为y=﹣x+3,直线C′D′解析式为y=﹣x+1.设点A的坐标为(m,2m),点D坐标为(0,n).
当A点在直线C′D′上时,有2m=﹣m+1,解得:m=![]() ,此时点A的坐标为(
,此时点A的坐标为(![]() ,
,![]() ),∴k=
),∴k=![]() ×
×![]() =
=![]() ;
;
当点D在直线A′B′上时,有n=3,此时点A的坐标为(3,6),∴k=3×6=18.
综上可知:当变化的正方形ABCD与(1)中的正方形A′B′C′D′有重叠部分时,k的取值范围为![]() ≤k≤18.故答案为:
≤k≤18.故答案为:![]() ≤k≤18.
≤k≤18.


科目:初中数学 来源: 题型:
【题目】如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程
(1)在方程①3x﹣1=0,②x﹣(3x+1)=﹣7中,不等式组![]() 的关联方程是 ;(填序号)
的关联方程是 ;(填序号)
(2)若不等式组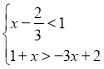 的一个关联方程的解是整数,则这个关联方程可以是 ;(写出一个即可)
的一个关联方程的解是整数,则这个关联方程可以是 ;(写出一个即可)
(3)若方程10﹣3x=2x,1+x=2(x﹣1)都是关于x的不等式组![]() 的关联方程,求出m的取值范围.
的关联方程,求出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.

(1)判断直线l与⊙O的位置关系,并说明理由;
(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;
(3)在(2)的条件下,若DE=4,DF=3,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过![]() 上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
(1)求证:△ECF∽△GCE;
(2)求证:EG是⊙O的切线;
(3)延长AB交GE的延长线于点M,若tanG=![]() ,AH=
,AH=![]() ,求EM的值.
,求EM的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组织340名师生进行长途考察活动,带有行李170件,计划租用甲、乙两种型号的汽车共10辆.经了解,甲车每辆最多能载40人和16件行李,乙车每辆最多能载30人和20件行李.
(1)请你帮助学校设计所有可行的租车方案.
(2)如果甲车的租金为每辆2 000元,乙车的租金为每辆1 800元,问哪种可行方案使租车费用最省?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》记载“今有邑方不知大小,各中开门.出北门三十步有木,出西门七百五十步见木.问邑方有几何?”意思是:如图,点M、点N分别是正方形ABCD的边AD、AB的中点,ME⊥AD,NF⊥AB,EF过点A,且ME=30步,NF=750步,则正方形的边长为( )
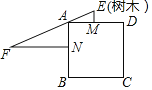
A. 150步B. 200步C. 250步D. 300步
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科技改变世界.2017年底,快递分拣机器人从微博火到了朋友圈.据介绍,这些机器人不仅可以自动规划最优路线,将包裹准确地放入相应的路口,还会感应避让障碍物,自动归队取包裹,没电的时候还会自己找充电桩充电.某快递公司启用40台A种机器人、150台B种机器人分拣快递包裹,A、B两种机器人全部投入工作,1小时共可以分拣0.77万件包裹;若全部A种机器人工作1.5小时,全部B种机器人工作2小时,一共可以分拣1.38万件包裹.
(1)求两种机器人每台每小时各分拣多少件包裹?
(2)为进一步提高效率,快递公司计划再购进A、B两种机器人共100台.若要保证新购进的这批机器人每小时的总分拣量不少于5500件,求至少应购进A种机器人多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中,装有2个红球,1个白球,1个黄球,这些球除颜色外都相同.求下列事件的概率:
(1)搅匀后从中任意摸出1个球,恰好是红球;
(2)搅匀后从中任意摸出2个球,2个都是红球.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com