
【题目】一个不透明的袋子中,装有2个红球,1个白球,1个黄球,这些球除颜色外都相同.求下列事件的概率:
(1)搅匀后从中任意摸出1个球,恰好是红球;
(2)搅匀后从中任意摸出2个球,2个都是红球.
【答案】(1)![]() ;(2)
;(2) ![]()
【解析】试题分析:(1)直接根据概率的概念求解;
(2)根据题意展示所有6种等可能的结果,其中摸出两个球恰好是2个红球占1种,然后根据概率的概念计算即可.
试题解析:
(1)搅匀后从中任意摸出1个球,所有可能出现的结果共有4种,它们出现的可能性相同.所有的结果中,满足“恰好是红球”(记为事件A)的结果有2种,
所以P(A)=![]() =
=![]() .
.
(2)搅匀后从中任意摸出2个球,所有可能出现的结果有:(红1,红2)、(红1,黄)、(红2,黄)、(红1,白)、(红2,白)、(白,黄),共有6种,它们出现的可能性相同.所有的结果中,满足“2个都是红球”(记为事件B)的结果只有1种,所以P(B)=![]() .
.
点睛:用列举法计算概率时,要注意求出事件发生情况的数目及其中一个事件发生的数目,而且每一种情况发生的可能性都相同,需要一次操作即可完成的事件,用概率公式来求解;需要两次或两次以上的操作完成的事件,先用列表法或画树状图法列举所有等可能的情况,再利用概率计算公式求解.


科目:初中数学 来源: 题型:
【题目】根据绝对值定义,若有![]() ,则
,则![]() 或
或![]() ,若
,若![]() ,则
,则![]() ,我们可以根据这样的结论,解一些简单的绝对值方程,例如:
,我们可以根据这样的结论,解一些简单的绝对值方程,例如:![]()
解:方程![]() 可化为:
可化为:
![]() 或
或![]()
当![]() 时, 则有:
时, 则有:![]() ; 所以
; 所以 ![]() .
.
当![]() 时, 则有:
时, 则有:![]() ;所以
;所以 ![]() .
.
故,方程![]() 的解为
的解为![]() 或
或![]() 。
。
(1)解方程:![]()
(2)已知![]() ,求
,求![]() 的值;
的值;
(3)在 (2)的条件下,若![]() 都是整数,则
都是整数,则![]() 的最大值是 (直接写结果,不需要过程).
的最大值是 (直接写结果,不需要过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
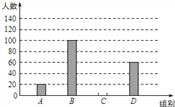
【题目】国家规定“中小学生每天在校体育活动时间不低于1小时”.为此,我区就“你每天在校体育活动时间是多少”的问题随机调查了区内300名初中学生.根据调查结果绘制成的统计图(部分)如图所示,其中分组情况是:
A组:t<0.5h B组:0.5h≤t<1h C组:1h≤t<1.5h D组:t≥1.5h
请根据上述信息解答下列问题:
(1)C组的人数是 .
(2)本次调查数据的中位数落在 组内;
(3)若我区有5400名初中学生,请你估计其中达国家规定体育活动时间的人约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
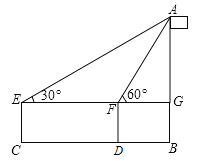
【题目】如图,小丽准备测一根旗杆AB的高度,已知小丽的眼睛离地面的距离EC=1.5米,第一次测量点C和第二次测量点D之间的距离CD=10米,∠AEG=30°,∠AFG=60°,请你帮小丽计算出这根旗杆的高度.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
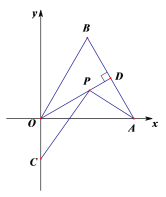
【题目】如图,在平面直角坐标系中,![]() OAB是边长为4的等边三角形,OD是AB边上的高,点P是OD上的一个动点,若点C的坐标是
OAB是边长为4的等边三角形,OD是AB边上的高,点P是OD上的一个动点,若点C的坐标是![]() ,则PA+PC的最小值是_________________.
,则PA+PC的最小值是_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产480个零件.当生产任务完成一半时,停止生产进行反思和改进,用时20分钟.恢复生产后工作效率比原来可以提高20%,要求比原计划提前40分钟完成任务,那么反思改进后每小时需要生产多少个零件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)
为了加强学生课外阅读,开阔视野,某校开展了“书香校园,从我做起”的主题活动.学校随机抽取了部分学生,对他们一周的课外阅读时间进行调查,绘制出频数分布表和频数分布直方图的一部分如下:


请根据图表信息回答下列问题:
(1)频数分布表中的![]() ,
,![]() ;
;
(2)将频数分布直方图补充完整;
(3)学校将每周课外阅读时间在![]() 小时以上的学生评为“阅读之星”,请你估计该校
小时以上的学生评为“阅读之星”,请你估计该校![]() 名学生中评为“阅读之星”的有多少人?
名学生中评为“阅读之星”的有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com