
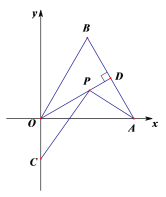
【题目】如图,在平面直角坐标系中,![]() OAB是边长为4的等边三角形,OD是AB边上的高,点P是OD上的一个动点,若点C的坐标是
OAB是边长为4的等边三角形,OD是AB边上的高,点P是OD上的一个动点,若点C的坐标是![]() ,则PA+PC的最小值是_________________.
,则PA+PC的最小值是_________________.
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】某超市销售一种牛奶,进价为每箱24元,规定售价不低于进价.现在的售价为每箱36元,每月可销售60箱.市场调查发现:若这种牛奶的售价每降价1元,则每月的销量将增加10箱,设每箱牛奶降价x元(x为正整数),每月的销量为y箱.
(1)写出y与x中间的函数关系式和自变量![]() 的取值范围;
的取值范围;
(2)超市如何定价,才能使每月销售牛奶的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
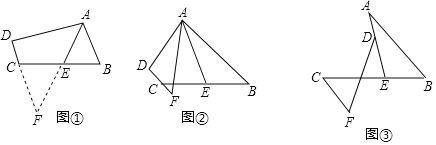
【题目】(1)阅读理解:如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC,得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断.
AB、AD、DC之间的等量关系为 ;
(2)问题探究:如图②,在四边形ABCD中,AB∥DC,AF与DC的延长线交于点F,E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.
(3)问题解决:如图③,AB∥CF,AE与BC交于点E,BE:EC=2:3,点D在线段AE上,且∠EDF=∠BAE,试判断AB、DF、CF之间的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
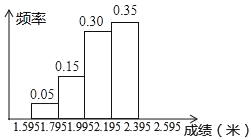
【题目】为了增强学生的身体素质,某校坚持长年的全员体育锻炼,并定期进行体能测试,下面是将某班学生的立定跳远成绩(精确到0.01m),进行整理后,分成5组,画了的频率分布直方图的部分,已知:从左到右4个小组的频率分别是:0.05,0.15,0.30,0.35,第五小组的频数是9.
(1)该班参加测试的人数是多少?
(2)补全频率分布直方图.
(3)若该成绩在2.00m(含2.00)的为合格,问该班成绩合格率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中,装有2个红球,1个白球,1个黄球,这些球除颜色外都相同.求下列事件的概率:
(1)搅匀后从中任意摸出1个球,恰好是红球;
(2)搅匀后从中任意摸出2个球,2个都是红球.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ABC为等边三角形,点D、E分别在直线AB、BC上,且AD=BE.
ABC为等边三角形,点D、E分别在直线AB、BC上,且AD=BE.
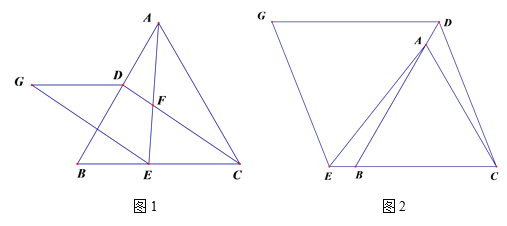
(1)如图1,若点D、E分别是AB、CB边上的点,连接AE、CD交于点F,过点E作∠AEG=60°,使EG=AE,连接GD,则∠AFD= (填度数);
(2)在(1)的条件下,猜想DG与CE存在什么关系,并证明;
(3)如图2,若点D、E分别是BA、CB延长线上的点,(2)中结论是否仍然成立?请给出判断并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E为 BC上的点,F为 CD边上的点,且AE=AF,AB=4,设EC=x,△AEF 的面积为y,则y与x之间的函数关系式是____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “清明时节雨纷纷”是必然事件
B. 了解路边行人边步行边低头看手机的情况可以采取对在路边行走的学生随机发放问卷的方式进行调查
C. 射击运动员甲、乙分别射击10次且击中环数的方差分别是0.5和1.2,则甲队员的成绩好
D. 分别写有三个数字 -1,-2,4的三张卡片(卡片的大小形状都相同),从中任意抽取两张,则卡片上的两数之积为正数的概率为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com