
【题目】某超市销售一种牛奶,进价为每箱24元,规定售价不低于进价.现在的售价为每箱36元,每月可销售60箱.市场调查发现:若这种牛奶的售价每降价1元,则每月的销量将增加10箱,设每箱牛奶降价x元(x为正整数),每月的销量为y箱.
(1)写出y与x中间的函数关系式和自变量![]() 的取值范围;
的取值范围;
(2)超市如何定价,才能使每月销售牛奶的利润最大?最大利润是多少元?
【答案】(1)y=60+10x,x为x≤12的正整数.
(2)当超市降价3元时,即每箱33元时,所获利润最大,最大利润为810元.
【解析】试题分析:(1)根据价格每降低1元,平均每天多销售10箱,由每箱降价x元,多卖10x,据此可以列出函数关系式;(2)由利润=(售价﹣成本)×销售量列出函数关系式,求出最大值.
试题解析:(1)根据题意,得:y=60+10x,由36﹣x≥24得x≤12,
∴1≤x≤12,且x为整数;
(2)设所获利润为W,
则W=(36﹣x﹣24)(10x+60)=﹣10x2+60x+720=﹣10(x﹣3)2+810,
∴当x=3时,W取得最大值,最大值为810,
答:超市定价为33元时,才能使每月销售牛奶的利润最大,最大利润是810元.


科目:初中数学 来源: 题型:
【题目】小张准备把一根长为32cm的铁丝剪成两段,并把每一段各围成一个正方形.(1)要使这两个正方形的面积之和等于40cm2,小张该怎么剪?
(2)小李对小张说:“这两个正方形的面积之和不可能等于30cm2.”他的说法对吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组发现一个结论:已知直线a∥b,若直线c∥a,则c∥b.他们发现这个结论运用很广,请你利用这个结论解决以下问题:

已知直线AB∥CD,点E在AB、CD之间,点P、Q分别在直线AB、CD上,连接PE、EQ.
(1)如图1,运用上述结论,探究∠PEQ与∠APE+∠CQE之间的数量关系,并说明理由;
(2)如图2,PF平分∠BPE,QF平分∠EQD,当∠PEQ=140°时,求出∠PFQ的度数;
(3)如图3,若点E在CD的下方,PF平分∠BPE,QH平分∠EQD,QH的反向延长线交PF于点F.当∠PEQ=70°时,请求出∠PFQ的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,对角线
中,对角线![]() 交于点
交于点![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.下列结论正确的是( )
的中点.下列结论正确的是( )
①![]() ;②
;②![]() ;③
;③![]() 平分
平分![]() ;④
;④![]() 平分
平分![]() ;⑤四边形
;⑤四边形![]() 是菱形.
是菱形.
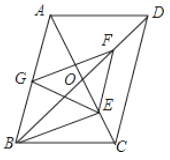
A.③⑤B.①②④C.①②③④D.①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在崇仁一中中学生篮球赛中,小方共打了10场球.他在第6,7,8,9场比赛中分别得了22,15,12和19分,他的前9场比赛的平均得分y比前5场比赛的平均得分x要高 .如果他所参加的10场比赛的平均得分超过18分
(1)用含x的代数式表示y;
(2)小方在前5场比赛中,总分可达到的最大值是多少?
(3)小方在第10场比赛中,得分可达到的最小值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
已知:如图,△ABC及AC边的中点O。
求作:平行四边形ABCD。

小敏的作法如下:
①连接BO并延长,在延长线上截取OD=BO;
②连接DA,DC.

所以四边形ABCD就是所求作的平行四边形.
老师说:“小敏的作法正确.”
请回答:小敏的作法正确的理由是_________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
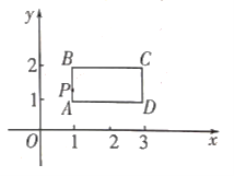
【题目】如图,在直角坐标系中,有一矩形![]() ,长
,长![]() ,宽
,宽![]()
![]() 轴,
轴,![]() 轴.点
轴.点![]() 坐标为
坐标为![]() ,该矩形边上有一动点
,该矩形边上有一动点![]() ,沿
,沿![]() 运动一周,则点
运动一周,则点![]() 的纵坐标
的纵坐标![]() 与点
与点![]() 走过的路程
走过的路程![]() 之间的函数关系用图象表示大致是( )
之间的函数关系用图象表示大致是( )
A.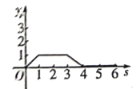 B.
B.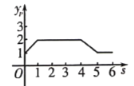
C.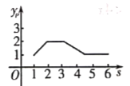 D.
D.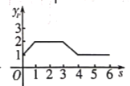
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】含60°角的菱形A1B1C1B2,A2B2C2B3,A3B3C3B4,…,按如图的方式放置在平面直角坐标系xOy中,点A1,A2,A3,…,和点B1,B2,B3,B4,…,分别在直线y=kx和x轴上.已知B1(2,0),B2(4,0),则点A1的坐标是_____;点A3的坐标是_____;点An的坐标是____(n为正整数).
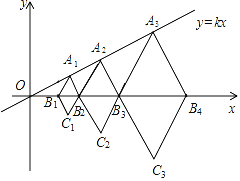
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com