
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
已知:如图,△ABC及AC边的中点O。
求作:平行四边形ABCD。

小敏的作法如下:
①连接BO并延长,在延长线上截取OD=BO;
②连接DA,DC.

所以四边形ABCD就是所求作的平行四边形.
老师说:“小敏的作法正确.”
请回答:小敏的作法正确的理由是_________________________________.
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,△ABC的三个顶点分别是A(-2,0),B(0,3),C(3,0).
(1)在所给的图中,画出这个平面直角坐标系;
(2)点A经过平移后对应点为D(3,-3),将△ABC作同样的平移得到△DEF,点B的对应点为点E,画出平移后的△DEF;
(3)在(2)的条件下,点M在直线CD上,若DM=2CM,直接写出点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】标有-3,-2,4的三张不透明的卡片,除正面写有不同的数字外,其余的值都相同,将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记为一次函数解析式y=kx+b的k值,第二次从余下的两张卡片中再抽取一张,上面标有的数字记为一次函数解析式的b值.
(1)写出k为负数的概率;
(2)求一次函数y=kx+b的图象不经过第一象限的概率.(用树状图或列举法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种牛奶,进价为每箱24元,规定售价不低于进价.现在的售价为每箱36元,每月可销售60箱.市场调查发现:若这种牛奶的售价每降价1元,则每月的销量将增加10箱,设每箱牛奶降价x元(x为正整数),每月的销量为y箱.
(1)写出y与x中间的函数关系式和自变量![]() 的取值范围;
的取值范围;
(2)超市如何定价,才能使每月销售牛奶的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“爱满扬州”慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成统计图.

(1)这50名同学捐款的众数为 元,中位数为 元;
(2)求这50名同学捐款的平均数;
(3)该校共有600名学生参与捐款,请估计该校学生的捐款总数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用硬纸板剪一个平行四边形ABCD,作出它的对角线的交点O,我们可以做如下操作:
用大头针把一根平放在平行四边形上的直细木条固定在点O处,并使细木条可以绕点O转动,拨动细木条,它可以停留在任意位置. 如果设细木条与一组对边AB,CD的交点分别为点E,F,则下列结论:①OE=OF;②AE=CF;③BE=DF;④△AOE≌△COF,其中一定成立的是_________________________(填写序号即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=kx-2与坐标轴所围图形的面积为3,点A(3,m)是直线y=kx-2上一点.
(1)求点A的坐标;
(2)点P在y轴上,且∠PAO=30°,直接写出点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
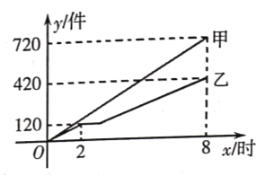
【题目】六一儿童节来临之际,某服装厂要加工一批服装捐赠给贫困山区的孩子们该厂甲、乙两个车间同时开工赶制这批服装,从开始加工到加工完这批服装,甲车间连续工作了![]() 小时,乙车间中途停工一段时间维修设备,修好后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止如图,是甲、乙两个车间各自加工的服装数量
小时,乙车间中途停工一段时间维修设备,修好后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止如图,是甲、乙两个车间各自加工的服装数量![]() (件)与时间
(件)与时间![]() (时)的函数图象.
(时)的函数图象.
![]() 甲、乙两车间一共加工的服装件数是 件;甲车间每小时加工服装的件数是 件.
甲、乙两车间一共加工的服装件数是 件;甲车间每小时加工服装的件数是 件.
![]() 乙车间中途停工维修设备用了多长时间?
乙车间中途停工维修设备用了多长时间?
![]() 求乙车间维修设备后,乙车间加工服装的数量
求乙车间维修设备后,乙车间加工服装的数量![]() 与
与![]() 之间的函数表达式
之间的函数表达式
![]() 开工后多长时间,甲、乙两个车间共同完成了
开工后多长时间,甲、乙两个车间共同完成了![]() 件服装的加工.
件服装的加工.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,分别过
,分别过![]() 、
、![]() 两点作过点
两点作过点![]() 的直线
的直线![]() 的垂线,垂足为
的垂线,垂足为![]() 、
、![]() ;
;

(1)如图1,当![]() 、
、![]() 两点在直线
两点在直线![]() 的同侧时,猜想,
的同侧时,猜想,![]() 、
、![]() 、
、![]() 三条线段有怎样的数量关系?并说明理由.
三条线段有怎样的数量关系?并说明理由.
(2)如图2,当![]() 、
、![]() 两点在直线
两点在直线![]() 的两侧时,
的两侧时,![]() 、
、![]() 、
、![]() 三条线段有怎样的数量关系?并说明理由.
三条线段有怎样的数量关系?并说明理由.
(3)如图3,![]() ,
,![]() ,
,![]() .点
.点![]() 从
从![]() 点出发沿
点出发沿![]() 路径向终点
路径向终点![]() 运动;点
运动;点![]() 从
从![]() 点出发沿
点出发沿![]() 路径向终点
路径向终点![]() 运动.点
运动.点![]() 和
和![]() 分别以每秒2和3个单位的速度同时开始运动,只要有一点到达相应的终点时两点同时停止运动;在运动过程中,分别过
分别以每秒2和3个单位的速度同时开始运动,只要有一点到达相应的终点时两点同时停止运动;在运动过程中,分别过![]() 和
和![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]() .问:点
.问:点![]() 运动多少秒时,
运动多少秒时,![]() 与
与![]() 全等?(直接写出结果即可)
全等?(直接写出结果即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com