
【题目】某学习小组发现一个结论:已知直线a∥b,若直线c∥a,则c∥b.他们发现这个结论运用很广,请你利用这个结论解决以下问题:

已知直线AB∥CD,点E在AB、CD之间,点P、Q分别在直线AB、CD上,连接PE、EQ.
(1)如图1,运用上述结论,探究∠PEQ与∠APE+∠CQE之间的数量关系,并说明理由;
(2)如图2,PF平分∠BPE,QF平分∠EQD,当∠PEQ=140°时,求出∠PFQ的度数;
(3)如图3,若点E在CD的下方,PF平分∠BPE,QH平分∠EQD,QH的反向延长线交PF于点F.当∠PEQ=70°时,请求出∠PFQ的度数.
【答案】(1)∠PEQ=∠APE+∠CQE,理由见解析;(2)∠PFQ=110°;(3)∠PFQ=145°.
【解析】
(1)
过E点作EH∥AB,再利用平行线性质,两直线平行内错角相等,可得到∠PEQ=∠APE+∠CQE.
(2)过点E作EM∥AB,利用平行线性质,角平分线定义可以得到角的关系,可得到∠PEQ=∠APE+∠CQE=140°,再作NF∥AB,利用平行线性质,角平分线定义可以得到角的关系,得到,∠PFQ=∠BPF+∠DQF的度数.
(3)过点E作EM∥CD,如图,设∠CQM=α,∴∠DQE=180°-α,再利用角平分线性质得到∠DQH=90°-![]() α,∠FQD=90°+
α,∠FQD=90°+![]() α,再利用平行线性质、角平分线定义∠BPF=
α,再利用平行线性质、角平分线定义∠BPF=![]() ∠BPE=55°-
∠BPE=55°-![]() α,作NF∥AB,∠PFQ=∠BPF+∠DQF即可求出答案.
α,作NF∥AB,∠PFQ=∠BPF+∠DQF即可求出答案.
(1)
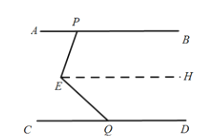
过E点作EH∥AB,
∠PEQ=∠APE+∠CQE,理由如下:
过点E作EH∥AB ∴∠APE=∠PEH ∵EH∥AB,AB∥CD ∴EH∥CD
∴∠CQE=∠QEH,∵∠PEQ=∠PEH+∠QEH ∴∠PEQ=∠APE+∠CQE
(2)
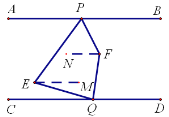
过点E作EM∥AB,如图,同理可得,∠PEQ=∠APE+∠CQE=140°
∵∠BPE=180°-∠APE,∠EQD=180°-∠CQE,∴∠BPE+∠EQD=360°-(∠APE+∠CQE)=220°,∵PF平分∠BPE,QF平分∠EQD ∴∠BPF=![]() ∠BPE,∠DQF=
∠BPE,∠DQF=![]() ∠EQD
∠EQD
∴∠BPF+∠DQF=![]() (∠BPE+∠EQD)=110°,作NF∥AB,同理可得,∠PFQ=∠BPF+∠DQF=110°
(∠BPE+∠EQD)=110°,作NF∥AB,同理可得,∠PFQ=∠BPF+∠DQF=110°
(3)
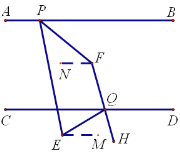
过点E作EM∥CD,如图,设∠CQM=α,∴∠DQE=180°-α,∵QH平分∠DQE,
∴∠DQH=![]() ∠DQE=90°-
∠DQE=90°-![]() α,∴∠FQD=180°-∠DQH=90°+
α,∴∠FQD=180°-∠DQH=90°+![]() α,
α,
∵EM∥CD,AB∥CD ∴AB∥EM,∴∠BPE=180°-∠PEM=180°-(70°+α)=110°-α
∵PF平分∠BPE ∴∠BPF=![]() ∠BPE=55°-
∠BPE=55°-![]() α,
α,
作NF∥AB,同理可得,∠PFQ=∠BPF+∠DQF=145°


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】某校组织学生书法比赛,对参赛作品按A、B、C、D四个等级进行了评定.现随机取部分学生书法作品的评定结果进行分析,并绘制扇形统计图和条形统计图如下:

根据上述信息完成下列问题:
(1)求这次抽取的样本的容量;
(2)请在图②中把条形统计图补充完整;
(3)已知该校这次活动共收到参赛作品750份,请你估计参赛作品达到B级以上(即A级和B级)有多少份?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,△ABC的三个顶点分别是A(-2,0),B(0,3),C(3,0).
(1)在所给的图中,画出这个平面直角坐标系;
(2)点A经过平移后对应点为D(3,-3),将△ABC作同样的平移得到△DEF,点B的对应点为点E,画出平移后的△DEF;
(3)在(2)的条件下,点M在直线CD上,若DM=2CM,直接写出点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为∠A,∠B,∠C所对的边,我们称关于x的一元二次方程![]() 为“△ABC的☆方程”.根据规定解答下列问题:
为“△ABC的☆方程”.根据规定解答下列问题:
(1)“△ABC的☆方程” ![]() 的根的情况是______(填序号):
的根的情况是______(填序号):
①有两个相等的实数根;②有两个不相等的实数根;③没有实数根;
(2)如图,AD为⊙O的直径,BC为弦, BC⊥AD于E,∠DBC=30°,求“△ABC的☆方程” ![]() 的解;
的解;

(3)若x=![]() 是“△ABC的☆方程”
是“△ABC的☆方程” ![]() 的一个根,其中a,b,c均为整数,且
的一个根,其中a,b,c均为整数,且![]() ,求方程的另一个根.
,求方程的另一个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次课题学习活动中,老师提出了如下问题:如图,四边形![]() 是正方形,点
是正方形,点![]() 是边
是边![]() 的中点,
的中点,![]() ,且
,且![]() 交正方形外角平分线
交正方形外角平分线![]() 于点
于点![]() .请你探究
.请你探究![]() 与
与![]() 存在怎样的数量关系,并证明你的结论正确.经过探究,小明得出的结论是
存在怎样的数量关系,并证明你的结论正确.经过探究,小明得出的结论是![]() ,而要证明结论
,而要证明结论![]() ,就需要证明
,就需要证明![]() 和
和![]() 所在的两个三角形全等,但
所在的两个三角形全等,但![]() 和
和![]() 显然不全等(一个是直角三角形,一个是钝角三角形),考虑到点
显然不全等(一个是直角三角形,一个是钝角三角形),考虑到点![]() 是边
是边![]() 的中点,小明想到的方法是如图2,取
的中点,小明想到的方法是如图2,取![]() 的中点
的中点![]() ,连接
,连接![]() ,证明
,证明![]() .从而得到
.从而得到![]() .请你参考小明的方法解决下列问题.
.请你参考小明的方法解决下列问题.
(1)如图3,若把条件“点![]() 是边
是边![]() 的中点”改为“点
的中点”改为“点![]() 是边
是边![]() 上的任意一点”,其余条件不变,证明结论
上的任意一点”,其余条件不变,证明结论![]() 仍然成立;
仍然成立;
(2)如图4,若把条件“点![]() 是边
是边![]() 的中点”改为:“点
的中点”改为:“点![]() 是边
是边![]() 延长线上的一点”,其余条件仍不变,那么结论
延长线上的一点”,其余条件仍不变,那么结论![]() 是否还成立?若成立,请完成证明过程,若不成立,请说明理由.
是否还成立?若成立,请完成证明过程,若不成立,请说明理由.




查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小林在某商店购买商品A、B共三次,只有一次购买时,商品A、B同时打折(折扣相同),其余两次均按标价购买.三次购买商品A、B的数量和费用如下表:
购买商品A的数量/个 | 购买商品B的数量/个 | 购买总费用/元 | |
第一次购物 | 6 | 5 | 1140 |
第二次购物 | 3 | 7 | 1110 |
第三次购物 | 9 | 8 | 1062 |
(1)小林以折扣价购买商品A、B是第 次购物;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】标有-3,-2,4的三张不透明的卡片,除正面写有不同的数字外,其余的值都相同,将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记为一次函数解析式y=kx+b的k值,第二次从余下的两张卡片中再抽取一张,上面标有的数字记为一次函数解析式的b值.
(1)写出k为负数的概率;
(2)求一次函数y=kx+b的图象不经过第一象限的概率.(用树状图或列举法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种牛奶,进价为每箱24元,规定售价不低于进价.现在的售价为每箱36元,每月可销售60箱.市场调查发现:若这种牛奶的售价每降价1元,则每月的销量将增加10箱,设每箱牛奶降价x元(x为正整数),每月的销量为y箱.
(1)写出y与x中间的函数关系式和自变量![]() 的取值范围;
的取值范围;
(2)超市如何定价,才能使每月销售牛奶的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
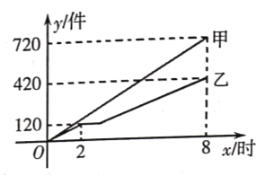
【题目】六一儿童节来临之际,某服装厂要加工一批服装捐赠给贫困山区的孩子们该厂甲、乙两个车间同时开工赶制这批服装,从开始加工到加工完这批服装,甲车间连续工作了![]() 小时,乙车间中途停工一段时间维修设备,修好后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止如图,是甲、乙两个车间各自加工的服装数量
小时,乙车间中途停工一段时间维修设备,修好后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止如图,是甲、乙两个车间各自加工的服装数量![]() (件)与时间
(件)与时间![]() (时)的函数图象.
(时)的函数图象.
![]() 甲、乙两车间一共加工的服装件数是 件;甲车间每小时加工服装的件数是 件.
甲、乙两车间一共加工的服装件数是 件;甲车间每小时加工服装的件数是 件.
![]() 乙车间中途停工维修设备用了多长时间?
乙车间中途停工维修设备用了多长时间?
![]() 求乙车间维修设备后,乙车间加工服装的数量
求乙车间维修设备后,乙车间加工服装的数量![]() 与
与![]() 之间的函数表达式
之间的函数表达式
![]() 开工后多长时间,甲、乙两个车间共同完成了
开工后多长时间,甲、乙两个车间共同完成了![]() 件服装的加工.
件服装的加工.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com