
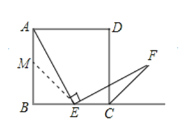
【题目】在一次课题学习活动中,老师提出了如下问题:如图,四边形![]() 是正方形,点
是正方形,点![]() 是边
是边![]() 的中点,
的中点,![]() ,且
,且![]() 交正方形外角平分线
交正方形外角平分线![]() 于点
于点![]() .请你探究
.请你探究![]() 与
与![]() 存在怎样的数量关系,并证明你的结论正确.经过探究,小明得出的结论是
存在怎样的数量关系,并证明你的结论正确.经过探究,小明得出的结论是![]() ,而要证明结论
,而要证明结论![]() ,就需要证明
,就需要证明![]() 和
和![]() 所在的两个三角形全等,但
所在的两个三角形全等,但![]() 和
和![]() 显然不全等(一个是直角三角形,一个是钝角三角形),考虑到点
显然不全等(一个是直角三角形,一个是钝角三角形),考虑到点![]() 是边
是边![]() 的中点,小明想到的方法是如图2,取
的中点,小明想到的方法是如图2,取![]() 的中点
的中点![]() ,连接
,连接![]() ,证明
,证明![]() .从而得到
.从而得到![]() .请你参考小明的方法解决下列问题.
.请你参考小明的方法解决下列问题.
(1)如图3,若把条件“点![]() 是边
是边![]() 的中点”改为“点
的中点”改为“点![]() 是边
是边![]() 上的任意一点”,其余条件不变,证明结论
上的任意一点”,其余条件不变,证明结论![]() 仍然成立;
仍然成立;
(2)如图4,若把条件“点![]() 是边
是边![]() 的中点”改为:“点
的中点”改为:“点![]() 是边
是边![]() 延长线上的一点”,其余条件仍不变,那么结论
延长线上的一点”,其余条件仍不变,那么结论![]() 是否还成立?若成立,请完成证明过程,若不成立,请说明理由.
是否还成立?若成立,请完成证明过程,若不成立,请说明理由.




【答案】(1)正确,见解析;(2)正确,见解析
【解析】
(1)在AB上取点![]() ,连接
,连接![]() ,证明△PAE≌△CEF即可;
,证明△PAE≌△CEF即可;
(2)延长BA至![]() ,使
,使![]() =CE,连接
=CE,连接![]() ,证明△ANE≌△ECF即可.
,证明△ANE≌△ECF即可.
解:(1)正确.
证明:在AB上取一点M,使AM=EC,连接ME.
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]()
∴BM=BE,
∴∠BME=45°,
∴∠AME=135°,
∵CF是外角平分线,
∴∠DCF=45°,
∴∠ECF=135°,
∴∠AME=∠ECF,
∵∠AEB+∠BAE=90°,∠AEB+∠CEF=90°,
∴∠BAE=∠CEF,
∴△AME≌△ECF(ASA),
∴AE=EF.
(2)正确.
证明:在BA的延长线上取一点N.
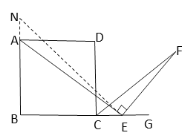
使AN=CE,连接NE.
∴BN=BE,
∴∠N=∠NEC=45°,
∵CF平分∠DCG,
∴∠FCE=45°,
∴∠N=∠ECF,
∵四边形ABCD是正方形,
∴AD∥BE,
∴∠DAE=∠BEA,
即∠DAE+90°=∠BEA+90°,
∴∠NAE=∠CEF,
∴△ANE≌△ECF(ASA)
∴AE=EF.


科目:初中数学 来源: 题型:
【题目】某种流感病毒,有一人患了这种流感,在每轮传染中一人将平均传给x人.
(1)求第一轮后患病的人数;(用含x的代数式表示)
(2)在进入第二轮传染之前,有两位患者被及时隔离并治愈,问第二轮传染后总共是否会有21人患病的情况发生,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,CD⊥BC,BD与AC相交于点E,AB=9,BC=4,DC=3.
(1)求BE的长度;
(2)求△ABE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.

(1)若花园的面积为192m2,求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求x取何值时,花园面积S最大,并求出花园面积S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
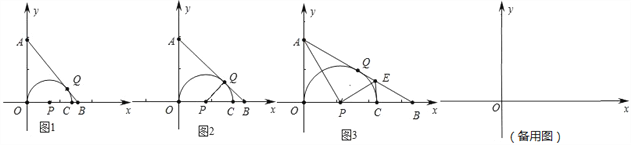
【题目】平面直角坐标系中,A(0,4),点P从原点O开始向x轴正方向运动,设P点横坐标为m,以点P为圆心,PO为半径作⊙P交x 轴另一点为C,过点A作⊙P的切线交 x轴于点B,切点为Q.
(1)如图1,当B点坐标为(3,0)时,求m;
(2)如图2,当△PQB为等腰三角形时,求m;
(3)如图3,连接AP,作PE⊥AP交AB于点E,连接CE,求证:CE是⊙P的切线;
(4)若在x轴上存在点M(8,0),在点P整个运动过程中,求MQ的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组发现一个结论:已知直线a∥b,若直线c∥a,则c∥b.他们发现这个结论运用很广,请你利用这个结论解决以下问题:

已知直线AB∥CD,点E在AB、CD之间,点P、Q分别在直线AB、CD上,连接PE、EQ.
(1)如图1,运用上述结论,探究∠PEQ与∠APE+∠CQE之间的数量关系,并说明理由;
(2)如图2,PF平分∠BPE,QF平分∠EQD,当∠PEQ=140°时,求出∠PFQ的度数;
(3)如图3,若点E在CD的下方,PF平分∠BPE,QH平分∠EQD,QH的反向延长线交PF于点F.当∠PEQ=70°时,请求出∠PFQ的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E。若DE=1,则BC的长为( )

A.2+![]() B.
B.![]() C.
C.![]() D.3
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
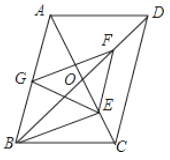
【题目】如图,![]() 中,对角线
中,对角线![]() 交于点
交于点![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.下列结论正确的是( )
的中点.下列结论正确的是( )
①![]() ;②
;②![]() ;③
;③![]() 平分
平分![]() ;④
;④![]() 平分
平分![]() ;⑤四边形
;⑤四边形![]() 是菱形.
是菱形.
A.③⑤B.①②④C.①②③④D.①②③④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com