
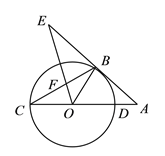
【题目】如图, ![]() 为⊙
为⊙![]() 的直径,点
的直径,点![]() 在⊙
在⊙![]() 上,连接
上,连接![]() 、
、![]() ,过点
,过点![]() 的切线
的切线![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,
, ![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
(![]() )求证:
)求证: ![]() .
.
(![]() )若⊙
)若⊙![]() 的半径为
的半径为![]() ,
, ![]() ,求
,求![]() 的长.
的长.
【答案】(![]() )见解析 (
)见解析 (![]() )
)![]() .
.
【解析】(1)连接OB.由切线的性质先证明∠OBE=∠EFB+∠CBO=90°,再由圆周角定理得出∠CBD=∠CBO+∠OBD=90°,故∠EBF=∠OBD,根据等腰三角形的性质可知∠OBD=∠CDB,故∠EBF=∠CDB,进而可得结论;
(2)由(1)可知![]() ∽
∽![]() ∠OBE=90°,∠E=∠C,在Rt△BOE中,利用锐角三角函数的定义即可得出结论.
∠OBE=90°,∠E=∠C,在Rt△BOE中,利用锐角三角函数的定义即可得出结论.
证明:(![]() )∵
)∵![]() ,∴
,∴![]() ,
, ![]() (两直线平行,内错角相等,同位角相等).
(两直线平行,内错角相等,同位角相等).
连接![]() ,
,
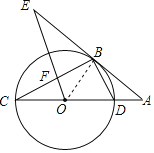
∵过点![]() 的切线
的切线![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,
,
∴OB⊥AE,
∴∠OBE=∠EFB+∠CBO=90°,
![]() 为⊙
为⊙![]() 的直径,
的直径,
∴∠CBD=∠CBO+∠OBD=90°,
∴∠EBF=∠OBD,
∵OB、OD是⊙O的半径,
∴OB=OD,
∴∠OBD=∠CDB,
∴∠EBF=∠CDB,
∵![]() ,
,
∴∠EFB=∠CBD,
∴![]() ∽
∽![]() .
.
(![]() )由1)可知
)由1)可知![]() ∽
∽![]()
∴∠OBE=90°,
∴∠E=∠C,
∵∠C=30°,
∴∠E=∠C=30°,
∵⊙O的半径为3,
在Rt△BOE中,∠OBE=90°,∠E =30°,OB=3,
∴![]() ,即
,即![]() ,
,
∴![]() 的长为
的长为![]() .
.


科目:初中数学 来源: 题型:
【题目】在一次课题学习活动中,老师提出了如下问题:如图,四边形![]() 是正方形,点
是正方形,点![]() 是边
是边![]() 的中点,
的中点,![]() ,且
,且![]() 交正方形外角平分线
交正方形外角平分线![]() 于点
于点![]() .请你探究
.请你探究![]() 与
与![]() 存在怎样的数量关系,并证明你的结论正确.经过探究,小明得出的结论是
存在怎样的数量关系,并证明你的结论正确.经过探究,小明得出的结论是![]() ,而要证明结论
,而要证明结论![]() ,就需要证明
,就需要证明![]() 和
和![]() 所在的两个三角形全等,但
所在的两个三角形全等,但![]() 和
和![]() 显然不全等(一个是直角三角形,一个是钝角三角形),考虑到点
显然不全等(一个是直角三角形,一个是钝角三角形),考虑到点![]() 是边
是边![]() 的中点,小明想到的方法是如图2,取
的中点,小明想到的方法是如图2,取![]() 的中点
的中点![]() ,连接
,连接![]() ,证明
,证明![]() .从而得到
.从而得到![]() .请你参考小明的方法解决下列问题.
.请你参考小明的方法解决下列问题.
(1)如图3,若把条件“点![]() 是边
是边![]() 的中点”改为“点
的中点”改为“点![]() 是边
是边![]() 上的任意一点”,其余条件不变,证明结论
上的任意一点”,其余条件不变,证明结论![]() 仍然成立;
仍然成立;
(2)如图4,若把条件“点![]() 是边
是边![]() 的中点”改为:“点
的中点”改为:“点![]() 是边
是边![]() 延长线上的一点”,其余条件仍不变,那么结论
延长线上的一点”,其余条件仍不变,那么结论![]() 是否还成立?若成立,请完成证明过程,若不成立,请说明理由.
是否还成立?若成立,请完成证明过程,若不成立,请说明理由.




查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“爱满扬州”慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成统计图.

(1)这50名同学捐款的众数为 元,中位数为 元;
(2)求这50名同学捐款的平均数;
(3)该校共有600名学生参与捐款,请估计该校学生的捐款总数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=kx-2与坐标轴所围图形的面积为3,点A(3,m)是直线y=kx-2上一点.
(1)求点A的坐标;
(2)点P在y轴上,且∠PAO=30°,直接写出点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
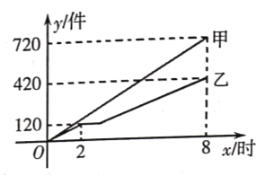
【题目】六一儿童节来临之际,某服装厂要加工一批服装捐赠给贫困山区的孩子们该厂甲、乙两个车间同时开工赶制这批服装,从开始加工到加工完这批服装,甲车间连续工作了![]() 小时,乙车间中途停工一段时间维修设备,修好后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止如图,是甲、乙两个车间各自加工的服装数量
小时,乙车间中途停工一段时间维修设备,修好后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止如图,是甲、乙两个车间各自加工的服装数量![]() (件)与时间
(件)与时间![]() (时)的函数图象.
(时)的函数图象.
![]() 甲、乙两车间一共加工的服装件数是 件;甲车间每小时加工服装的件数是 件.
甲、乙两车间一共加工的服装件数是 件;甲车间每小时加工服装的件数是 件.
![]() 乙车间中途停工维修设备用了多长时间?
乙车间中途停工维修设备用了多长时间?
![]() 求乙车间维修设备后,乙车间加工服装的数量
求乙车间维修设备后,乙车间加工服装的数量![]() 与
与![]() 之间的函数表达式
之间的函数表达式
![]() 开工后多长时间,甲、乙两个车间共同完成了
开工后多长时间,甲、乙两个车间共同完成了![]() 件服装的加工.
件服装的加工.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
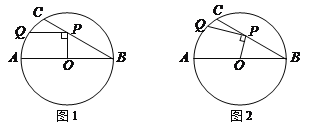
(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
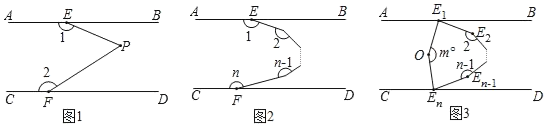
【题目】(提出问题)(1)如图1,已知AB∥CD,证明:∠1+∠EPF+∠2=360°;
(类比探究)(2)如图2,已知AB∥CD,设从E点出发的(n﹣1)条折线形成的n个角分别为∠1,∠2……∠n,探索∠1+∠2+∠3+……+∠n的度数可能在1700°至2000°之间吗?若有可能请求出n的值,若不可能请说明理由.
(拓展延伸)(3)如图3,已知AB∥CD,∠AE1E2的角平分线E1O与∠CEnEn﹣1的角平分线EnO交于点O,若∠E1OEn=m°.求∠2+∠3+∠4+…+∠(n﹣1)的度数.(用含m、n的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com