
【题目】小张准备把一根长为32cm的铁丝剪成两段,并把每一段各围成一个正方形.(1)要使这两个正方形的面积之和等于40cm2,小张该怎么剪?
(2)小李对小张说:“这两个正方形的面积之和不可能等于30cm2.”他的说法对吗?请说明理由.
【答案】(1)小张应将40cm的铁丝剪成8cm和24cm两段,并将每一段围成一个正方形;(2)他的说法对.
【解析】试题分析:
(1)设围成的两个正方形中其中一个边长为xcm,则另一个正方形的边长为![]() cm,由此根据题意可列出方程
cm,由此根据题意可列出方程![]() ,解此方程即可;
,解此方程即可;
(2)同(1)可得方程: ![]() ,化为一般形式由“一元二次方程根的判别式”可知该方程无实数根,从而可得结论;
,化为一般形式由“一元二次方程根的判别式”可知该方程无实数根,从而可得结论;
试题分析:
(1)设其中一个正方形的边长为xcm,则另一个正方形的边长为(8﹣x)cm.
∴x2+(8﹣x)2=40,
即x2﹣8x+12=0.
∴x1=2,x2=6.
∴当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ;
;
∴一个正方形的周长为8cm,另一个正方形的周长为24cm,
∴小张应将40cm的铁丝剪成8cm和24cm两段,并将每一段围成一个正方形.
(2)他的说法对.
假定两个正方形的面积之和能等于30cm2.
根据(1)中的方法,可得x2+(8﹣x)2=30.
即x2﹣8x+17=0,
∵△=82﹣4×17<0,
∴所列方程无解.
∴两个正方形的面积之和不可能等于30cm2.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案科目:初中数学 来源: 题型:
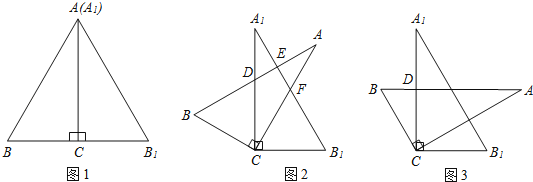
【题目】将两块全等的含30°角的直角三角板按图1的方式放置,已知∠BAC=∠B1A1C=30°,AB=2BC.
(1)固定三角板A1B1C,然后将三角板ABC绕点C顺时针方向旋转至图2的位置,AB与A1C、A1B1分别交于点D、E,AC与A1B1交于点F.
①填空:当旋转角等于20°时,∠BCB1= 度;
②当旋转角等于多少度时,AB与A1B1垂直?请说明理由.
(2)将图2中的三角板ABC绕点C顺时针方向旋转至图3的位置,使AB∥CB1,AB与A1C交于点D,试说明A1D=CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生书法比赛,对参赛作品按A、B、C、D四个等级进行了评定.现随机取部分学生书法作品的评定结果进行分析,并绘制扇形统计图和条形统计图如下:

根据上述信息完成下列问题:
(1)求这次抽取的样本的容量;
(2)请在图②中把条形统计图补充完整;
(3)已知该校这次活动共收到参赛作品750份,请你估计参赛作品达到B级以上(即A级和B级)有多少份?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某品牌的饮料有大瓶与小瓶装之分.某超市花了2100元购进一批该品牌的饮料共800瓶,其中,大瓶和小瓶饮料的进价及售价如右表所示.
大瓶 | 小瓶 | |
进价(元/瓶) |
|
|
售价(元/瓶) |
|
|
(1)问:该超市购进大瓶和小瓶饮料各多少瓶?
(2)当大瓶饮料售出了200瓶,小瓶饮料售出了100瓶后,商家决定将剩下的小瓶饮料的售价降低0.5元销售,并把其中一定数量的小瓶饮料作为赠品,在顾客一次性购买大瓶饮料时,每满2瓶就送1瓶小瓶饮料,送完即止.请问:超市要使这批饮料售完后获得的利润为1075元,那么小瓶饮料作为赠品送出多少瓶?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 边的垂直平分线
边的垂直平分线![]() 交
交![]() 于点
于点![]() ,
,![]() 边的垂直平分线
边的垂直平分线![]() 交
交![]() 于点
于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,联结
,联结![]() 、
、![]() ,若
,若![]() 的周长为
的周长为![]() ,
,![]() 的周长为
的周长为![]() .
.

(1)求线段![]() 的长;
的长;
(2)联结![]() ,求线段
,求线段![]() 的长;
的长;
(3)若![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是长方形,∠A=∠ABC=∠BCD=∠CDA=90°,AB∥CD,AD∥BC,E是边AD上一动点.
(1)若∠ECD=2∠ECB,求∠AEC的度数.
(2)若∠ABD=70°,△DEF是等腰三角形,求∠ECB的度数.
(3)若△EFD的面积为4,若△DCF的面积为6,则四边形ABFE的面积为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,△ABC的三个顶点分别是A(-2,0),B(0,3),C(3,0).
(1)在所给的图中,画出这个平面直角坐标系;
(2)点A经过平移后对应点为D(3,-3),将△ABC作同样的平移得到△DEF,点B的对应点为点E,画出平移后的△DEF;
(3)在(2)的条件下,点M在直线CD上,若DM=2CM,直接写出点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为∠A,∠B,∠C所对的边,我们称关于x的一元二次方程![]() 为“△ABC的☆方程”.根据规定解答下列问题:
为“△ABC的☆方程”.根据规定解答下列问题:
(1)“△ABC的☆方程” ![]() 的根的情况是______(填序号):
的根的情况是______(填序号):
①有两个相等的实数根;②有两个不相等的实数根;③没有实数根;
(2)如图,AD为⊙O的直径,BC为弦, BC⊥AD于E,∠DBC=30°,求“△ABC的☆方程” ![]() 的解;
的解;

(3)若x=![]() 是“△ABC的☆方程”
是“△ABC的☆方程” ![]() 的一个根,其中a,b,c均为整数,且
的一个根,其中a,b,c均为整数,且![]() ,求方程的另一个根.
,求方程的另一个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种牛奶,进价为每箱24元,规定售价不低于进价.现在的售价为每箱36元,每月可销售60箱.市场调查发现:若这种牛奶的售价每降价1元,则每月的销量将增加10箱,设每箱牛奶降价x元(x为正整数),每月的销量为y箱.
(1)写出y与x中间的函数关系式和自变量![]() 的取值范围;
的取值范围;
(2)超市如何定价,才能使每月销售牛奶的利润最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com