
【题目】已知![]() ABC为等边三角形,点D、E分别在直线AB、BC上,且AD=BE.
ABC为等边三角形,点D、E分别在直线AB、BC上,且AD=BE.
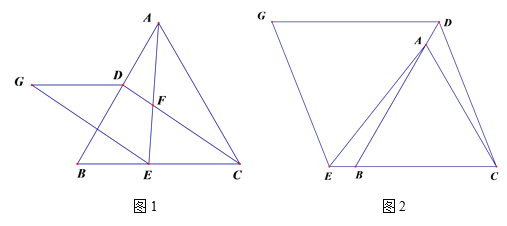
(1)如图1,若点D、E分别是AB、CB边上的点,连接AE、CD交于点F,过点E作∠AEG=60°,使EG=AE,连接GD,则∠AFD= (填度数);
(2)在(1)的条件下,猜想DG与CE存在什么关系,并证明;
(3)如图2,若点D、E分别是BA、CB延长线上的点,(2)中结论是否仍然成立?请给出判断并证明.
【答案】(1)∠AFD= 60°(2)DG=CE,DG//CE;(3)详见解析
【解析】
(1) 证明△ABE≌△CAD(SAS),可得 ∠BAE=∠ACD,继而根据等边三角形的内角为60度以及三角形外角的性质即可求得答案;
(2)由(1)∠AFD=60°,根据∠AEG=60°,可得GE//CD ,继而根据GE=AE=CD,可得四边形GECD是平行四边形,根据平行四边形的性质即可得DG=CE,DG//CE;
(3)延长EA交CD于点F,先证明△ACD≌△BAE,根据全等三角形的性质可得 ∠ACD=∠BAE, CD=AE,继而根据三角形外角的性质可得到∠EFC= 60°,从而得∠EFC=∠GEF,得到GE//CD,继而证明四边形GECD是平行四边形 ,根据平行四边形的性质即可得到DG=CE,DG//CE.
(1) ∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠ABC=60°,
在△ABE和△CAD中,
 ,
,
∴△ABE≌△CAD(SAS),
∴∠BAE=∠ACD,
∵∠BAE+∠EAC=∠BAC=60°,
∴∠ACD+∠EAC=60°,
∴∠AFD=∠ACD+∠EAC=60°,
故答案为:60° ;
(2)DG=CE,DG//CE,理由如下:
∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠ABC=60°,
在△ABE和△CAD中,
 ,
,
∴△ABE≌△CAD(SAS),
∴AE=CD,∠BAE=∠ACD,
∵∠BAE+∠EAC=∠BAC=60°,
∴∠ACD+∠EAC=60°,
∴∠AFD=∠ACD+∠EAC=60°,
又∵∠AEG=60°,
∴∠AFD=∠AEG,
∴GE//CD ,
∵GE=AE=CD,
∴四边形GECD是平行四边形,
∴DG=CE,DG//CE;
(3)仍然成立
延长EA交CD于点F,
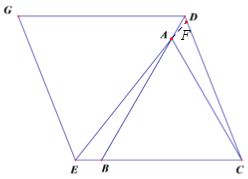
∵△ABC为等边三角形,
∴AC=AB,∠BAC=∠ABC=60°,
∴∠DAC=∠ABE=120°,
在△ACD和△BAE中,
 ,
,
∴△ACD≌△BAE(SAS),
∴∠ACD=∠BAE, CD=AE,
∴∠EFC=∠DAF+∠BDC=∠BAE +∠AEB=∠ABC= 60°,
∴∠EFC=∠GEF,
∴GE//CD,
∵GE=AE=CD,
∴四边形GECD是平行四边形 ,
∴DG=CE,DG//CE.


科目:初中数学 来源: 题型:
【题目】如图1,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.
(1)判断BF与AC的数量关系并说明理由;
(2)如图2,将△ACD沿线段AD对折,点C落在BD上的点M,AM与BE相交于点N,当DE∥AM时,判断NE与AC的数量关系并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国元朝朱世杰所著的《算学启蒙》(1299年)一书中有一道题目是:“今有良马日行二百四十里,驽马日行一百五十里.驽马先行一十二日,问良马几何日追及之.”译文是:快马每天走240里,慢马每天走150里.慢马先走12天,快马几天可以追上慢马?
(1)设快马x天可以追上慢马,请你将如下的线段图补充完整:
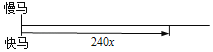
(2)根据(1)中线段图所反映的数量关系,列方程解决问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 是⊙
是⊙![]() 的直径,点
的直径,点![]() 是⊙
是⊙![]() 上一点,
上一点, ![]() 与过点
与过点![]() 的切线垂直,垂足为点
的切线垂直,垂足为点![]() ,直线
,直线![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() ,弦
,弦![]() 平分∠
平分∠![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
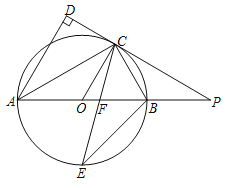
(1)求证: ![]() 平分∠
平分∠![]() ;
;
(2)求证:PC=PF;
(3)若![]() ,AB=14,求线段
,AB=14,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
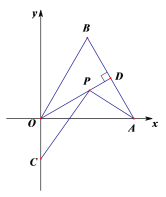
【题目】如图,在平面直角坐标系中,![]() OAB是边长为4的等边三角形,OD是AB边上的高,点P是OD上的一个动点,若点C的坐标是
OAB是边长为4的等边三角形,OD是AB边上的高,点P是OD上的一个动点,若点C的坐标是![]() ,则PA+PC的最小值是_________________.
,则PA+PC的最小值是_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为(![]() ,﹣2);⑤当x<
,﹣2);⑤当x<![]() 时,y随x的增大而减小;⑥a+b+c>0中,其中正确的有( )
时,y随x的增大而减小;⑥a+b+c>0中,其中正确的有( )

A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
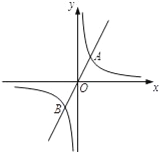
【题目】如图,正比例函数y=2x的图象与反比例函数y=![]() 的图象交于点A、B,AB=2
的图象交于点A、B,AB=2![]() ,
,
(1)求k的值;
(2)若反比例函数y=![]() 的图象上存在一点C,则当△ABC为直角三角形,请直接写出点C的坐标.
的图象上存在一点C,则当△ABC为直角三角形,请直接写出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发门市销售两种商品,甲种商品每件售价为300元,乙种商品每件售价为80元.新年来临之际,该门市为促销制定了两种优惠方案:
方案一:买一件甲种商品就赠送一件乙种商品;
方案二:按购买金额打八折付款.
某公司为奖励员工,购买了甲种商品20件,乙种商品x(x≥20)件.
(1)分别写出优惠方案一购买费用y1(元)、优惠方案二购买费用y2(元)与所买乙种商品x(件)之间的函数关系式;
(2)若该公司共需要甲种商品20件,乙种商品40件.设按照方案一的优惠办法购买了m件甲种商品,其余按方案二的优惠办法购买.请你写出总费用w与m之间的关系式;利用w与m之间的关系式说明怎样购买最实惠.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com