
【题目】二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为(![]() ,﹣2);⑤当x<
,﹣2);⑤当x<![]() 时,y随x的增大而减小;⑥a+b+c>0中,其中正确的有( )
时,y随x的增大而减小;⑥a+b+c>0中,其中正确的有( )

A. 2个B. 3个C. 4个D. 5个
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
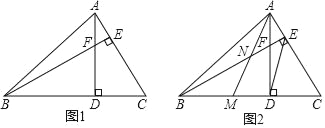
【题目】如图1,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.
(1)判断BF与AC的数量关系并说明理由;
(2)如图2,将△ACD沿线段AD对折,点C落在BD上的点M,AM与BE相交于点N,当DE∥AM时,判断NE与AC的数量关系并说明理由.
【答案】(1)BF=AC,理由见解析;(2)NE=![]() AC,理由见解析.
AC,理由见解析.
【解析】试题分析:(1)如图1,证明△ADC≌△BDF(AAS),可得BF=AC;
(2)如图2,由折叠得:MD=DC,先根据三角形中位线的推论可得:AE=EC,由线段垂直平分线的性质得:AB=BC,则∠ABE=∠CBE,结合(1)得:△BDF≌△ADM,则∠DBF=∠MAD,最后证明∠ANE=∠NAE=45°,得AE=EN,所以EN=![]() AC.
AC.
试题解析:
(1)BF=AC,理由是:
如图1,∵AD⊥BC,BE⊥AC,
∴∠ADB=∠AEF=90°,
∵∠ABC=45°,
∴△ABD是等腰直角三角形,
∴AD=BD,
∵∠AFE=∠BFD,
∴∠DAC=∠EBC,
在△ADC和△BDF中,
∵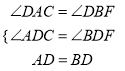 ,
,
∴△ADC≌△BDF(AAS),
∴BF=AC;
(2)NE=![]() AC,理由是:
AC,理由是:
如图2,由折叠得:MD=DC,
∵DE∥AM,
∴AE=EC,
∵BE⊥AC,
∴AB=BC,
∴∠ABE=∠CBE,
由(1)得:△ADC≌△BDF,
∵△ADC≌△ADM,
∴△BDF≌△ADM,
∴∠DBF=∠MAD,
∵∠DBA=∠BAD=45°,
∴∠DBA﹣∠DBF=∠BAD﹣∠MAD,
即∠ABE=∠BAN,
∵∠ANE=∠ABE+∠BAN=2∠ABE,
∠NAE=2∠NAD=2∠CBE,
∴∠ANE=∠NAE=45°,
∴AE=EN,
∴EN=![]() AC.
AC.
【题型】解答题
【结束】
17
【题目】已知x1,x2是方程2x2﹣2nx+![]() n(n+4)=0的两根,且(x1﹣1)(x2﹣1)﹣1=
n(n+4)=0的两根,且(x1﹣1)(x2﹣1)﹣1=![]() ,求n的值.
,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如下图所示,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:①b2-4ac>0;②abc<0;③m>2.其中,正确结论的个数是

A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在直角坐标系中,A(﹣2,4)B(﹣4,2);A1、B1是A、B关于y轴的对称点;
(1)请在图中画出A、B关于原点O的对称点A2,B2(保留痕迹,不写作法);并直接写出A1、A2、B1、B2的坐标.
(2)试问:在x轴上是否存在一点C,使△A1B1C的周长最小,若存在求C点的坐标,若不存在说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
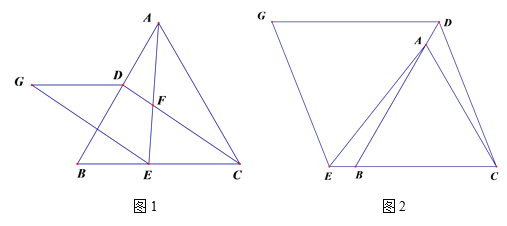
【题目】已知![]() ABC为等边三角形,点D、E分别在直线AB、BC上,且AD=BE.
ABC为等边三角形,点D、E分别在直线AB、BC上,且AD=BE.
(1)如图1,若点D、E分别是AB、CB边上的点,连接AE、CD交于点F,过点E作∠AEG=60°,使EG=AE,连接GD,则∠AFD= (填度数);
(2)在(1)的条件下,猜想DG与CE存在什么关系,并证明;
(3)如图2,若点D、E分别是BA、CB延长线上的点,(2)中结论是否仍然成立?请给出判断并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
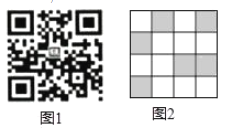
【题目】利用如图1的二维码可以进行身份识别,某校建立了一个身份识别系绕,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0,将第一行数字从左到右依次记为a,b,c,d,那么可以转换为该生所在班级序号,其序号为a×23+b×22+c×21+d×20,如图2第一行数字从左到右依次为0,1,0,1,序号为0×23+1×22+0×21+1×20=5,表示该生为5班学生,那么表示7班学生的识别图案是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师打算在小明和小白两位同学之间选一位同学参加数学竞赛,他收集了小明、小白近期10次数学考试成绩,并绘制了折线统计图(如图所示)
项目 | 众数 | 中位数 | 平均数 | 方差 | 最高分 |
小明 | 85 | 85 | |||
小白 | 70,100 | 85 | 100 |
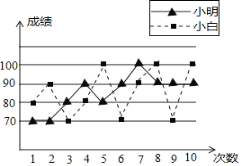
(1)根据折线统计图,张老师绘制了不完整的统计表,请你补充完整统计表;
(2)你认为张老师会选择哪位同学参加比赛?并说明你的理由
查看答案和解析>>
科目:初中数学 来源: 题型:
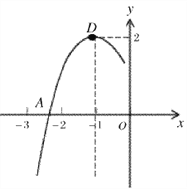
【题目】拋物线![]() 的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:①
的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:①![]() ;②当x>-l时,y随x增大而减小;③a+b+c<0;④若方程
;②当x>-l时,y随x增大而减小;③a+b+c<0;④若方程![]() 没有实数根,则m>2. 其中正确的结论有________________.
没有实数根,则m>2. 其中正确的结论有________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
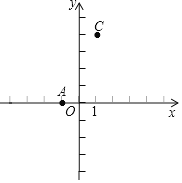
【题目】如图,![]() ,
,![]() ,点B在x轴上,且
,点B在x轴上,且![]() .
.
![]() 求点B的坐标;
求点B的坐标;
![]() 求
求![]() 的面积;
的面积;
![]() 在y轴上是否存在P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请求出点P的坐标;若不存在,请说明理由.
在y轴上是否存在P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com