
【题目】张老师打算在小明和小白两位同学之间选一位同学参加数学竞赛,他收集了小明、小白近期10次数学考试成绩,并绘制了折线统计图(如图所示)
项目 | 众数 | 中位数 | 平均数 | 方差 | 最高分 |
小明 | 85 | 85 | |||
小白 | 70,100 | 85 | 100 |
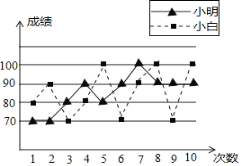
(1)根据折线统计图,张老师绘制了不完整的统计表,请你补充完整统计表;
(2)你认为张老师会选择哪位同学参加比赛?并说明你的理由
【答案】(1)90,90,100;85,145;(2) 选择小明同学,理由见解析.
【解析】
(1)先根据折线统计图得出两人的成绩,再根据众数、中位数、平均数和方差的定义计算可得;
(2)根据众数、中位数、平均数和方差的意义解答,合理即可得.
.解:(1)小明同学的成绩为:70、70、80、80、90、90、90、90、90、100,
所以小明成绩的众数为90、中位数为90、最高分为100;
小白同学的成绩为:70、70、70、80、80、90、90、100、100、100,
所以小白同学成绩的平均数为![]() =85,
=85,
则方差为![]() ×[3×(70﹣85)2+2×(80﹣85)2+2×(90﹣85)2+3×(100﹣85)2]=145,
×[3×(70﹣85)2+2×(80﹣85)2+2×(90﹣85)2+3×(100﹣85)2]=145,
补全表格如下:
项目 | 众数 | 中位数 | 平均数 | 方差 | 最高分 |
小明 | 90 | 90 | 85 | 85 | 100 |
小白 | 70,100 | 85 | 85 | 145 | 100 |
(2)选择小明同学,
∵小明、小白的平均成绩相同,而小明成绩的方差较小,发挥比较稳定,
∴选择小明同学参加比赛.


科目:初中数学 来源: 题型:
【题目】为了传承优秀传统文化,某校组织800名学生参加了一次“汉字听写”大赛.赛后发现所有参赛学生的成绩均不低于60分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩作为样本,成绩如下:
90,92,81,82,78,95,86,88,72,66,62,68,89,86,93,83,100,73,76,80,77,81,86,75,82,85,71,68,74,98,90,97,85,84,78,73,65,92,96,60
对上述成绩进行了整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
60≤x<70 | 6 | 0.15 |
70≤x<80 | a | b |
80≤x<90 | 14 | 0.35 |
90≤x≤100 | c | d |
请根据所给信息,解答下列问题:
(1)a= ,d= .
(2)请补全频数分布直方图
(3)若成绩在90分以上(包括90分)的为“优等,请你估计参加这次比赛的800名学生中成绩“优”等的约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 是⊙
是⊙![]() 的直径,点
的直径,点![]() 是⊙
是⊙![]() 上一点,
上一点, ![]() 与过点
与过点![]() 的切线垂直,垂足为点
的切线垂直,垂足为点![]() ,直线
,直线![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() ,弦
,弦![]() 平分∠
平分∠![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
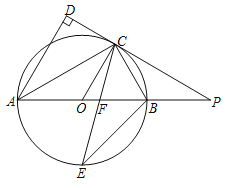
(1)求证: ![]() 平分∠
平分∠![]() ;
;
(2)求证:PC=PF;
(3)若![]() ,AB=14,求线段
,AB=14,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为(![]() ,﹣2);⑤当x<
,﹣2);⑤当x<![]() 时,y随x的增大而减小;⑥a+b+c>0中,其中正确的有( )
时,y随x的增大而减小;⑥a+b+c>0中,其中正确的有( )

A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正比例函数y=2x的图象与反比例函数y=![]() 的图象交于点A、B,AB=2
的图象交于点A、B,AB=2![]() ,
,
(1)求k的值;
(2)若反比例函数y=![]() 的图象上存在一点C,则当△ABC为直角三角形,请直接写出点C的坐标.
的图象上存在一点C,则当△ABC为直角三角形,请直接写出点C的坐标.
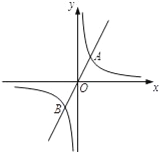
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AB上一点,D为AC的中点,E为BC的中点,F为DE的中点.
(1)若AC=4,BC=6,求CF的长.
(2)若AB=16CF,求![]() 的值.
的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知拋物线![]() (k为常数,且k>0)与x轴的交点为A、B,与y轴的交点为C,经过点B的直线
(k为常数,且k>0)与x轴的交点为A、B,与y轴的交点为C,经过点B的直线![]() 与抛物线的另一个交点为D.
与抛物线的另一个交点为D.
(1)若点D的横坐标为x= -4,求这个一次函数与抛物线的解析式;
(2)若直线m平行于该抛物线的对称轴,并且可以在线段AB间左右移动,它与直线BD和抛物线分别交于点E、F,求当m移动到什么位置时,EF的值最大,最大值是多少?
(3)问原抛物线在第一象限是否存在点P,使得△APB∽△ABC?若存在,请求出这时k的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年5月14日至15日,“一带一路”国际合作高峰论坛在北京举行,本届论坛期间,中国同30多个国家签署经贸合作协议,某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区. 已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.
(1)甲种商品与乙种商品的销售单价各多少元?
(2)若甲、乙两种商品的销售总收入不低于5400万元,则至少销售甲种商品多少万件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com