练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】我国元朝朱世杰所著的《算学启蒙》（1299年）一书中有一道题目是：“今有良马日行二百四十里，驽马日行一百五十里．驽马先行一十二日，问良马几何日追及之．”译文是：快马每天走240里，慢马每天走150里．慢马先走12天，快马几天可以追上慢马？

    （1）设快马x天可以追上慢马，请你将如下的线段图补充完整：

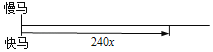
    （2）根据（1）中线段图所反映的数量关系，列方程解决问题．

    【答案】（1）见解析；（2）240x﹣150x＝150×12，快马20天可以追上慢马，见解析

    【解析】

    设快马x天可以追上慢马，根据慢马先行的路程＝快慢马速度之差×快马行走天数，即可列出关于x的一元一次方程，解之即可得出结论．

    解：（1）如图所示：

    （2）设快马x天可以追上慢马，

    由题意，得240x﹣150x＝150×12，

    解得：x＝20．

    答：快马20天可以追上慢马．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】为了打造铁力旅游景点，市旅游局打算将依吉密河中一段长1800米的河道整治任务交由甲、乙两个工程队来完成．已知，甲工程队每天整治60米，乙工程队每天整治40米．

    （1）若甲、乙两个工程队接龙来完成，共用时35天，求甲、乙两个工程队分别整治多长的河道？

    （2）若乙工程队先整治河道10天，甲工程队再参加两个工程队一起来完成剩余河道整治任务，求整段河道整治任务共用时多少天？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

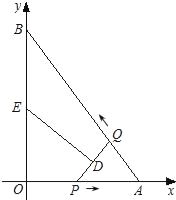
    【题目】如图，在平面直角坐标系xOy中，直线AB与x轴交于点A，与y轴交于点B，且OA=3，AB=5．点P从点O出发沿OA以每秒1个单位长的速度向点A匀速运动，到达点A后立刻以原来的速度沿AO返回；点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动．伴随着P、Q的运动，DE保持垂直平分PQ，且交PQ于点D，交折线QB﹣BO﹣OP于点E．点P、Q同时出发，当点Q到达点B时停止运动，点P也随之停止．设点P、Q运动的时间是t秒（t＞0）．

    （1）求直线AB的解析式；

    （2）在点P从O向A运动的过程中，求△APQ的面积S与t之间的函数关系式（不必写出t的取值范围）；

    （3）在点E从B向O运动的过程中，完成下面问题：

    ①四边形QBED能否成为直角梯形？若能，请求出t的值；若不能，请说明理由；

    ②当DE经过点O时，请你直接写出t的值．

    【答案】（1）直线AB的解析式为；（2）S=﹣t2+t；

    （3）四边形QBED能成为直角梯形．①t=；②当DE经过点O时，t=或．

    【解析】分析：（1）首先由在Rt△AOB中,OA=3,AB=5,求得OB的值，然后利用待定系数法即可求得一次函数的解析式；
    （2）过点Q作QF⊥AO于点F.由△AQF∽△ABO,根据相似三角形的对应边成比例，借助于方程即可求得QF的长，然后即可求得的面积S与t之间的函数关系式；
    （3）①分别从DE∥QB与PQ∥BO去分析，借助于相似三角形的性质，即可求得t的值；
    ②根据题意可知即时，则列方程即可求得t的值．

    详解：(1)在Rt△AOB中,OA=3,AB=5,由勾股定理得

    ∴A(3,0),B(0,4).

    设直线AB的解析式为y=kx+b.

    ∴.解得

    ∴直线AB的解析式为

    (2)如图1，过点Q作QF⊥AO于点F.

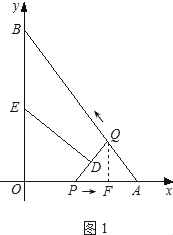
    ∵AQ=OP=t，∴AP=3t.

    由△AQF∽△ABO,得

    ∴

    ∴

    ∴

    ∴

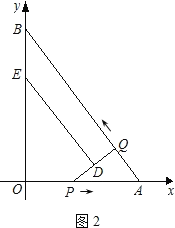
    (3)四边形QBED能成为直角梯形,

    ①如图2,当DE∥QB时，

    ∵DE⊥PQ，

    ∴PQ⊥QB，四边形QBED是直角梯形.

    此时

    由△APQ∽△ABO,得

    ∴

    解得

    如图3,当PQ∥BO时，

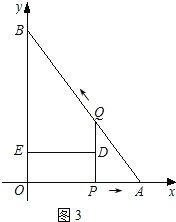
    ∵DE⊥PQ，

    ∴DE⊥BO，四边形QBED是直角梯形.

    此时

    由△AQP∽△ABO,得

    即

    3t=5(3t)，

    3t=155t，

    8t=15，

    解得

    (当P从A向0运动的过程中还有两个,但不合题意舍去).

    ②当DE经过点O时，

    ∵DE垂直平分PQ，

    ∴EP=EQ=t，

    由于P与Q相同的时间和速度，

    ∴AQ=EQ=EP=t，

    ∴∠AEQ=∠EAQ，

    ∵

    ∴∠BEQ=∠EBQ，

    ∴BQ=EQ，

    ∴

    所以

    当P从A向O运动时，

    过点Q作QF⊥OB于F，

    EP=6t,

    即EQ=EP=6t，

    AQ=t，BQ=5t，

    ∴

    ∴

    ∵

    即

    解得：

    ∴当DE经过点O时, 或.

    点睛：本题考查知识点较多，勾股定理，待定系数法求一次函数解析式，相似三角形的判定与性质等知识点，熟练掌握和运用各个知识点是解题的关键.

    【题型】解答题
    【结束】
    21

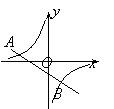
    【题目】如图，反比例函数y＝(m≠0)与一次函数y＝kx＋b(k≠0)的图象相交于A、B两点，点A的坐标为(－6，2)，点B的坐标为(3，n)．求反比例函数和一次函数的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在一个边长为a的正方形木板上锯掉一个边长为b的正方形, 并把余下的部分沿虚线剪开拼成图2的形状.

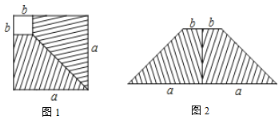
    (1)请用两种方法表示阴影部分的面积

    图1得： ； 图2得 ；

    (2)由图1与图2 面积关系，可以得到一个等式： ；

    (3)利用（2）中的等式，已知，且a+b=8，则a-b= .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

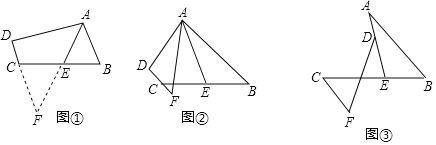
    【题目】（1）阅读理解：如图①，在四边形ABCD中，AB∥DC，E是BC的中点，若AE是∠BAD的平分线，试判断AB，AD，DC之间的等量关系．

    解决此问题可以用如下方法：延长AE交DC的延长线于点F，易证△AEB≌△FEC，得到AB=FC，从而把AB，AD，DC转化在一个三角形中即可判断．

    AB、AD、DC之间的等量关系为　 　；

    （2）问题探究：如图②，在四边形ABCD中，AB∥DC，AF与DC的延长线交于点F，E是BC的中点，若AE是∠BAF的平分线，试探究AB，AF，CF之间的等量关系，并证明你的结论．

    （3）问题解决：如图③，AB∥CF，AE与BC交于点E，BE：EC=2：3，点D在线段AE上，且∠EDF=∠BAE，试判断AB、DF、CF之间的数量关系，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如下图所示，且关于x的一元二次方程ax2+bx+c-m=0没有实数根，有下列结论：①b2-4ac>0；②abc<0；③m>2.其中，正确结论的个数是

    A. 0 B. 1 C. 2 D. 3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

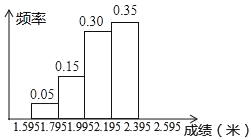
    【题目】为了增强学生的身体素质，某校坚持长年的全员体育锻炼，并定期进行体能测试，下面是将某班学生的立定跳远成绩（精确到0.01m），进行整理后，分成5组，画了的频率分布直方图的部分，已知：从左到右4个小组的频率分别是：0.05，0.15，0.30，0.35，第五小组的频数是9．

    （1）该班参加测试的人数是多少？

    （2）补全频率分布直方图．

    （3）若该成绩在2.00m（含2.00）的为合格，问该班成绩合格率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

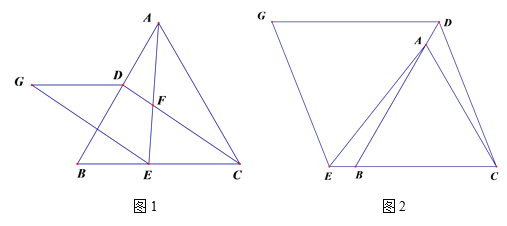
    【题目】已知ABC为等边三角形，点D、E分别在直线AB、BC上，且AD=BE.

    （1）如图1，若点D、E分别是AB、CB边上的点，连接AE、CD交于点F，过点E作∠AEG=60°，使EG=AE，连接GD，则∠AFD= （填度数）；

    （2）在（1）的条件下，猜想DG与CE存在什么关系，并证明；

    （3）如图2，若点D、E分别是BA、CB延长线上的点，（2）中结论是否仍然成立？请给出判断并证明.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

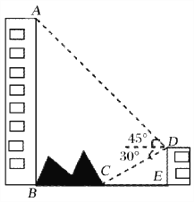
    【题目】如图，大楼底右侧有一障碍物，在障碍物的旁边有一幢小楼DE，在小楼的顶端D处测得障碍物边缘点C的俯角为30°，测得大楼顶端A的仰角为45°（点B，C，E在同一水平直线上）. 已知AB=80m，DE=10m，求障碍物B，C两点间的距离.（结果精确到0.1m）

    （参考数据: ，）

    查看答案和解析>>

    同步练习册答案