练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

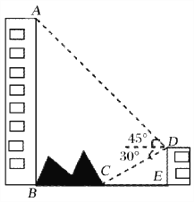
    【题目】如图，大楼底右侧有一障碍物，在障碍物的旁边有一幢小楼DE，在小楼的顶端D处测得障碍物边缘点C的俯角为30°，测得大楼顶端A的仰角为45°（点B，C，E在同一水平直线上）. 已知AB=80m，DE=10m，求障碍物B，C两点间的距离.（结果精确到0.1m）

    （参考数据: ，）

    【答案】52.7m

    【解析】分析：过点D作DF⊥AB于点F，过点C作CH⊥DF于点H，则DE=BF=CH=10m，根据直角三角形的性质得出DF的长．在Rt△CDE中，利用锐角三角函数的定义得出CE的长，根据BC=BE﹣CE即可得出结论．

    详解：过点D作DF⊥AB于点F，过点C作CH⊥DF于点H．

    则DE=BF=CH=10m．在Rt△ADF中，AF=AB﹣BF=70m，∠ADF=45°，∴DF=AF=70m．

    在Rt△CDE中，DE=10m，∠DCE=30°，∴CE===10（m），∴BC=BE﹣CE=（70﹣10）m．

    答：障碍物B，C两点间的距离为（70﹣10）m．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】我国元朝朱世杰所著的《算学启蒙》（1299年）一书中有一道题目是：“今有良马日行二百四十里，驽马日行一百五十里．驽马先行一十二日，问良马几何日追及之．”译文是：快马每天走240里，慢马每天走150里．慢马先走12天，快马几天可以追上慢马？

    （1）设快马x天可以追上慢马，请你将如下的线段图补充完整：

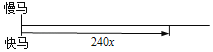
    （2）根据（1）中线段图所反映的数量关系，列方程解决问题．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

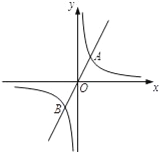
    【题目】如图，正比例函数y=2x的图象与反比例函数y=的图象交于点A、B，AB=2，

    （1）求k的值；

    （2）若反比例函数y=的图象上存在一点C，则当△ABC为直角三角形，请直接写出点C的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，等腰直角三角形中，，点是斜边上的一点，将沿翻折得，连接，若是等腰三角形，则的长是______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若一个整数能表示成a2＋b2（a、b是正整数）的形式，则称这个数为“完美数”。例如5是“完美数”，因为5＝22＋12，再如M＝x2＋2xy＋2y2=(x＋y)2 ＋y2（x、y是正整数），所以M也是“完美数”。

    （1）请你再写一个小于10的“完美数”，并判断29是否为“完美数”；

    （2）试判断(x2＋9y2)(4y2＋x2)（x、y是正整数）是否为“完美数”，并说明理由；

    （3）已知S＝x2＋4y2＋4x－12y＋k（x、y是正整数，k是常数），要使S为“完美数”，试求出符合条件的一个k值，并说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知拋物线（k为常数，且k＞0）与x轴的交点为A、B，与y轴的交点为C，经过点B的直线与抛物线的另一个交点为D.

    (1)若点D的横坐标为x= -4，求这个一次函数与抛物线的解析式；

    (2)若直线m平行于该抛物线的对称轴，并且可以在线段AB间左右移动，它与直线BD和抛物线分别交于点E、F，求当m移动到什么位置时，EF的值最大，最大值是多少？

    (3)问原抛物线在第一象限是否存在点P，使得△APB∽△ABC？若存在，请求出这时k的值；若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某天，一蔬菜经营户用114元从蔬菜批发市场购进黄瓜和土豆共40kg到菜市场去卖，黄瓜和土豆这天的批发价好零售价（单位：元/kg）如下表所示：

    品名

    批发价

    零售价

    黄瓜

    2.4

    4

    土豆

    3

    5

    （1）他当天购进黄瓜和土豆各多少千克？

    （2）如果黄瓜和土豆全部卖完，他能赚多少钱？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某批发门市销售两种商品，甲种商品每件售价为300元，乙种商品每件售价为80元.新年来临之际，该门市为促销制定了两种优惠方案：

    方案一：买一件甲种商品就赠送一件乙种商品；

    方案二：按购买金额打八折付款.

    某公司为奖励员工，购买了甲种商品20件，乙种商品x（x≥20）件.

    （1）分别写出优惠方案一购买费用y1（元）、优惠方案二购买费用y2（元）与所买乙种商品x（件）之间的函数关系式；

    （2）若该公司共需要甲种商品20件，乙种商品40件.设按照方案一的优惠办法购买了m件甲种商品，其余按方案二的优惠办法购买.请你写出总费用w与m之间的关系式；利用w与m之间的关系式说明怎样购买最实惠.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，锐角△ABC内接于⊙O，若⊙O的半径为6，sinA=，求BC的长．

    【答案】BC=8．

    【解析】试题分析：通过作辅助线构成直角三角形，再利用三角函数知识进行求解．

    试题解析：作⊙O的直径CD，连接BD，则CD=2×6=12.

    ∵

    ∴

    ∴

    点睛：直径所对的圆周角是直角.

    【题型】解答题
    【结束】
    22

    【题目】如图，一次函数y=k1x+b与反比例函数y=的图象交于A（2，m），B（n，﹣2）两点．过点B作BC⊥x轴，垂足为C，且S△ABC=5．

    （1）求一次函数与反比例函数的解析式；

    （2）根据所给条件，请直接写出不等式k1x+b＞的解集；

    （3）若P（p，y1），Q（﹣2，y2）是函数y=图象上的两点，且y1≥y2，求实数p的取值范围．

    查看答案和解析>>

    同步练习册答案