
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 平分
平分![]() 交于点
交于点![]() ,
,![]() 于点
于点![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④点
;④点![]() 在线段
在线段![]() 的垂直平分线上,其中正确的个数有( )
的垂直平分线上,其中正确的个数有( )
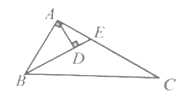
A.4个B.3个C.2个D.1个
【答案】A
【解析】
首先求出∠C=30°,∠ABC=60°,再根据角平分线的定义,直角三角形30°角的性质,线段的垂直平分线的定义一一判断即可.
∵在△ABC中,∠BAC=90°,∠ABC=2∠C,
∴∠C=30°,∠ABC=60°,
∵BE平分∠ABC,
∴∠ABE=∠EBC=30°,
∴∠EBC=∠C,
∴EB=EC,
∴AC-BE=AC-EC=AE,故①正确,
∵EB=EC,
∴点E在线段BC的垂直平分线上,故④正确,
∵AD⊥BE,
∴∠BAD=60°,
∵∠BAE=90°,
∴∠EAD=30°,
∴∠EAD=∠C,故②正确,
∵∠ABD=30°,∠ADB=90°,
∴AB=2AD,
∵∠BAC=90°,∠C=30°,
∴BC=2AB=4AD,故③正确,
故选A.


科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本),并指出售价为多少元时获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中,装有2个红球,1个白球,1个黄球,这些球除颜色外都相同.求下列事件的概率:
(1)搅匀后从中任意摸出1个球,恰好是红球;
(2)搅匀后从中任意摸出2个球,2个都是红球.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E为 BC上的点,F为 CD边上的点,且AE=AF,AB=4,设EC=x,△AEF 的面积为y,则y与x之间的函数关系式是____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,点D,E分别在AC,BC上,且CD·BC=AC·CE,以E为圆心,DE长为半径作圆,⊙E经过点B,与AB,BC分别交于点F,G.
(1)求证:AC是⊙E的切线;
(2)若AF=4,CG=5,
①求⊙E的半径;
②若Rt△ABC的内切圆圆心为I,则IE= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “清明时节雨纷纷”是必然事件
B. 了解路边行人边步行边低头看手机的情况可以采取对在路边行走的学生随机发放问卷的方式进行调查
C. 射击运动员甲、乙分别射击10次且击中环数的方差分别是0.5和1.2,则甲队员的成绩好
D. 分别写有三个数字 -1,-2,4的三张卡片(卡片的大小形状都相同),从中任意抽取两张,则卡片上的两数之积为正数的概率为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华将一条直角边长为1的一个等腰直角三角形纸片(如图1),沿它的对称轴折叠1次后得到一个等腰直角三角形(如图2),再将图2的等腰直角三角形沿它的对称轴折叠后得到一个等腰直角三角形(如图3),则图3中的等腰直角三角形的一条腰长为_________;同上操作,若小华连续将图1的等腰直角三角形折叠n次后所得到的等腰直角三角形(如图n+1)的一腰长为_________.
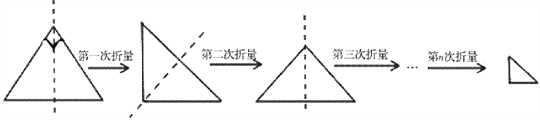
图1 图2 图3 图n+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣6,点B表示10,点C表示14,我们称点A和点C在数轴上相距20个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.
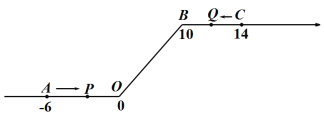
问:
(1)动点P从点A运动至C点需要时间为 秒;P、Q两点相遇时,求出相遇点M所对应的数是 ;
(2)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
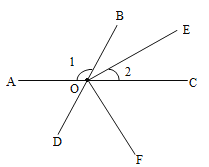
【题目】如图所示,点![]() 、
、![]() 、
、![]() 在同一直线上,
在同一直线上,![]() 是
是![]() 的平分线,
的平分线,![]() ,
,![]() ,
,![]() .
.
(1)求![]() 的度数(请写出解题过程).
的度数(请写出解题过程).
(2)如以![]() 为一边,在
为一边,在![]() 的外部画
的外部画![]() ,问边
,问边![]() 与边
与边![]() 成一直线吗?请说明理由.
成一直线吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com