
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本),并指出售价为多少元时获得最大利润,最大利润是多少?
【答案】(1)y=﹣2x+200;(2)售价为70元时获得最大利润,最大利润是1800元
【解析】试题分析: (1)待定系数法求解可得;
(2)根据“总利润=每千克利润×销售量”可得函数解析式,将其配方成顶点式即可得最值情况.
试题解析:(1)设y与x之间的函数解析式为y=kx+b,将(50,100),(60,80)分别代入表达式,得
![]() ,
,
解得![]() ,
,
即y与x之间的函数表达式是y=﹣2x+200;
(2)由题意可得,
W=(x﹣40)(﹣2x+200)=﹣2x2+280x﹣8000,
即W与x之间的函数表达式是W=﹣2x2+280x﹣8000;
∵W=﹣2x2+280x﹣8000=﹣2(x﹣70)2+1800,
∴当x=70时,W取得最大值,此时W=1800,
答:售价为70元时获得最大利润,最大利润是1800元.


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BD为一条对角线,AD//BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.
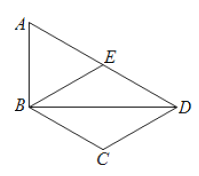
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,BC=1,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
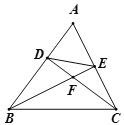
【题目】如图,在△ABC中,点D,E分别在边AB,AC上,且BE平分∠ABC,∠ABE=∠ACD,BE,CD交于点F.
(1)求证: ![]() ;
;
(2)请探究线段DE,CE的数量关系,并说明理由;
(3)若CD⊥AB,AD=2,BD=3,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据《居民家庭亲子阅读消费调查报告》中的相关数据制成扇形统计图,由图可知,下列说法错误的是( )

A.扇形统计图能反映各部分在总体中所占的百分比
B.每天阅读30分钟以上的居民家庭孩子超过50%
C.每天阅读1小时以上的居民家庭孩子占20%
D.每天阅读30分钟至1小时的居民家庭孩子对应扇形的圆心角是108°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解我市中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示.请根据图表信息解答下列问题:

(1)在表中:m= ,n= ;
(2)补全频数分布直方图;
(3)小明的成绩是所有被抽查学生成绩的中位数,据此推断他的成绩在 组;
(4)4个小组每组推荐1人,然后从4人中随机抽取2人参加颁奖典礼,恰好抽中A、C两组学生的概率是多少?并列表或画树状图说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019杨家埠民俗文化灯会于正月初一至二十(2.5-2.24)在杨家埠民间艺术大观园举办,此前,杨家埠民俗文化灯会已经成功举办了四届,每年入园游客达百万人次,极大地丰富了市民群众的春节文化生活.为了了解今年的游客构成情况,抽取了其中1天的数据进行调研.当天接待![]() 地游客0.9万人,
地游客0.9万人,![]() 地游客2.4万人,
地游客2.4万人,![]() 地游客2.1万人,
地游客2.1万人,![]() 地游客0.1万人,
地游客0.1万人,![]() 地游客情况如图所示,其扇形圆心角为
地游客情况如图所示,其扇形圆心角为![]() .
.
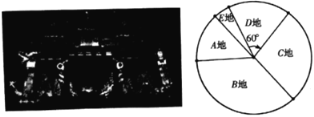
(1)抽到这一天当天的游客有多少人?
(2)当天A地游客占游客总数的百分比是多少?(精确到0.01%)
(3)当天C地游客在扇形统计图中的圆心角是多少度?(结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某巡警骑摩托车在一条南北大道上巡逻.某天他从岗亭出发,晚上停留在A处.规定向北方向为正.当天行驶记录如下(单位:千米).
+10,﹣8,+6,﹣13,+7,﹣12,+3,﹣2
(1)以岗亭为原点,用1个单位长度表示1KM,,在数轴上表示,A在岗亭何方,有多远?
(2)为该巡警巡逻时离岗亭最远是多少千米?
(3)在岗亭北面6千米处有个加油站,该巡警巡逻时经过加油站几次?
(4)若摩托车每行1千米耗油0.05升,那么该摩托车这天巡逻共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中有两条直线y=﹣2x+3和y=3x﹣2.
(1)确定这两条直线交点所在的象限,并说明理由;
(2)求两直线与坐标轴正半轴围成的四边形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)是否存在点M,使△OMC的面积是△OAC的面积的![]() ?若存在求出此时点M的坐标;若不存在,说明理由.
?若存在求出此时点M的坐标;若不存在,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com