[题目]2019杨家埠民俗文化灯会于正月初一至二十(2.5-2.24)在杨家埠民间艺术大观园举办.此前.杨家埠民俗文化灯会已经成功举办了四届.每年入园游客达百万人次.极大地丰富了市民群众的春节文化生活.为了了解今年的游客构成情况.抽取了其中1天的数据进行调研.当天接待地游客0.9万人.地游客2.4万人.地游客2.1万人.地游客0.1万人.地游客情况如图所示.其扇形圆题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】2019杨家埠民俗文化灯会于正月初一至二十（2.5-2.24）在杨家埠民间艺术大观园举办，此前，杨家埠民俗文化灯会已经成功举办了四届，每年入园游客达百万人次，极大地丰富了市民群众的春节文化生活.为了了解今年的游客构成情况，抽取了其中1天的数据进行调研.当天接待地游客0.9万人，地游客2.4万人，地游客2.1万人，地游客0.1万人，地游客情况如图所示，其扇形圆心角为.

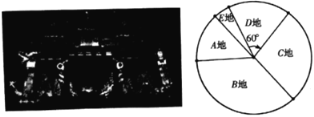
（1）抽到这一天当天的游客有多少人？

（2）当天A地游客占游客总数的百分比是多少？（精确到0.01%）

（3）当天C地游客在扇形统计图中的圆心角是多少度？（结果保留整数）

【答案】（1）总人数为6.6万人；（2）当天地游客占总游客数的百分比为；（3）当天C地游客的扇形圆心角度数为.

【解析】

（1）先求出D地所占总人数的百分比，然后得到其他四个地方的百分比，进而计算总人数；

（2）用A地的人数除以总人数即可；

（3）用360°乘以C地人数所占的百分比，即可得到答案.

解：（1）∵地游客为游客总数的，

∴除地游客外其余所有的游客为游客总数的，

∴总人数为：万人；

（2）当天地游客占总游客数的百分比为：；

（3）当天地游客的扇形圆心角度数为：.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

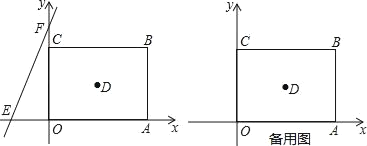
【题目】如图1，已知直角梯形ABCO中，∠AOC＝90°，AB∥x轴，AB＝6，若以O为原点，OA，OC所在直线为y轴和x轴建立如图所示直角坐标系，A(0，a)，C(c，0)中a，c满足|a+c﹣10|+＝0

（1）求出点A、B、C的坐标；

（2）如图2，若点M从点C出发，以2单位/秒的速度沿CO方向移动，点N从原点出发，以1单位/秒的速度沿OA方向移动，设M、N两点同时出发，且运动时间为t秒，当点N从点O运动到点A时，点M同时也停止运动，在它们的移动过程中，当2S△ABN≤S△BCM时，求t的取值范围：

（3）如图3，若点N是线段OA延长上的一动点，∠NCH＝k∠OCH，∠CNQ＝k∠BNQ，其中k＞1，NQ∥CJ，求的值（结果用含k的式子表示）．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，矩形ABCD中，AD=，F是DA延长线上一点，G是CF上一点，且∠ACG=∠AGC，∠GAF=∠F=20°，则AB=　　．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】（1）已知代数式（kx2+6x+8）-（6x+5x2+2）化简后的结果是常数，求系数k的值.

（2）先化简，再求值：2（-3xy-y2）-（2x2-7xy-2y2），其中x=3，y=-.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某超市销售一种商品，成本每千克40元，规定每千克售价不低于成本，且不高于80元，经市场调查，每天的销售量y（千克）与每千克售价x（元）满足一次函数关系，部分数据如下表：

售价x（元/千克）	50	60	70
销售量y（千克）	100	80	60

（1）求y与x之间的函数表达式；

（2）设商品每天的总利润为W（元），求W与x之间的函数表达式（利润=收入﹣成本），并指出售价为多少元时获得最大利润，最大利润是多少？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在平面直角坐标系中，正方形OABC的边长为a．直线y＝bx+c交x轴于E，交y轴于F，且a、b、c分别满足﹣（a﹣4）2≥0，c＝+8.

（1）求直线y＝bx+c的解析式并直接写出正方形OABC的对角线的交点D的坐标；

（2）直线y＝bx+c沿x轴正方向以每秒移动1个单位长度的速度平移，设平移的时间为t秒，问是否存在t的值，使直线EF平分正方形OABC的面积？若存在，请求出t的值；若不存在，请说明理由；

（3）点P为正方形OABC的对角线AC上的动点（端点A、C除外），PM⊥PO，交直线AB于M，求的值．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图1，四边形ABCD是正方形，AB=4，点G在BC边上，BG=3，DE⊥AG于点E，BF⊥AG于点F．

（1）求BF和DE的长；

（2）如图2，连接DF、CE，探究并证明线段DF与CE的数量关系与位置关系．

查看答案和解析>>

科目：初中数学 来源： 题型：

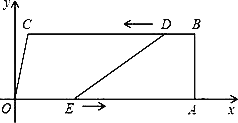
【题目】如图，在四边形OABC中，OA∥BC，∠OAB=90°，O为原点，点C的坐标为(2，8)，点A的坐标为(26，0)，点D从点B出发，以每秒1个单位长度的速度沿BC向点C运动，点E同时从点O出发，以每秒3个单位长度的速度沿折线OAB运动，当点E达到点B时，点D也停止运动，从运动开始，设D(E)点运动的时间为t秒．

(1)当t为何值时，四边形ABDE是矩形；

(2)当t为何值时，DE=CO？

(3)连接AD，记△ADE的面积为S，求S与t的函数关系式．