
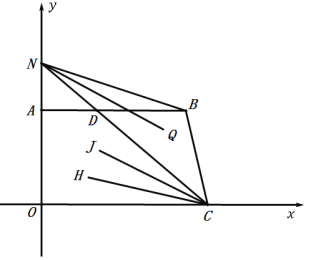
【题目】如图1,已知直角梯形ABCO中,∠AOC=90°,AB∥x轴,AB=6,若以O为原点,OA,OC所在直线为y轴和x轴建立如图所示直角坐标系,A(0,a),C(c,0)中a,c满足|a+c﹣10|+![]() =0
=0
(1)求出点A、B、C的坐标;
(2)如图2,若点M从点C出发,以2单位/秒的速度沿CO方向移动,点N从原点出发,以1单位/秒的速度沿OA方向移动,设M、N两点同时出发,且运动时间为t秒,当点N从点O运动到点A时,点M同时也停止运动,在它们的移动过程中,当2S△ABN≤S△BCM时,求t的取值范围:
(3)如图3,若点N是线段OA延长上的一动点,∠NCH=k∠OCH,∠CNQ=k∠BNQ,其中k>1,NQ∥CJ,求![]() 的值(结果用含k的式子表示).
的值(结果用含k的式子表示).

【答案】(1)A(0,3),B(6,3), C(7,0);(2)t的取值范围为2≤t≤3;(3)![]()
【解析】
(1)由绝对值和算术平方根的非负性质得出a+c﹣10=0,且c﹣7=0,求出c=7,a+c=10,得出c=3,即可得出答案;
(2)由题意得ON=t,CM=2t,得出AN=3﹣t,由2S△ABN≤S△BCM和三角形面积公式得出不等式,解得t≥2,由0≤t≤3,即可得出答案;
(3)设AB与CN交于点D,由平行线的性质结合三角形的外角性质和已知条件得出∠ABN=(k+1)(∠OCH﹣∠BNQ),再由平行线的性质和已知条件得出∠HCJ=k(∠OCH﹣∠BNQ),即可得出答案.
(1)∵![]()
![]()
![]()
∴![]() ,且
,且![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵AB∥![]() 轴,
轴,![]() ,
,
∴![]() ;
;
(2)∵![]() ,
,
∴![]() ,
,
由题意得:![]() ,
,
∴![]() ,
,
∵2S△ABN≤S△BCM,
∴![]() ,
,
解得:![]() ,
,
∵当点N从点O运动到点A时,点M同时也停止运动,
∴![]() ,
,
∴t的取值范围为:![]() ;
;
(3)设AB与CN交于点D,如图所示:
∵AB∥OC,
∴∠BDC=∠OCD,
∵∠BDC=∠BND+∠ABN,∠CNQ=k∠BNQ,∠NCH=k∠OCH,
∴∠BDC=(k+1)∠BNQ+∠ABN,∠OCD=(k+1)∠OCH,
∴(k+1)∠BNQ+∠ABN=(k+1)∠OCH,
∴∠ABN═(k+1)∠OCH﹣(k+1)∠BNQ=(k+1)(∠OCH﹣∠BNQ),
∵NQ∥CJ,
∴∠NCJ=∠CNQ=k∠BNQ,
∵∠HCJ+∠NCJ=∠NCH=k∠OCH,
∴∠HCJ=k∠OCH﹣∠NCJ=k∠OCH﹣k∠BNQ=k(∠OCH﹣∠BNQ),
∴![]() =
=![]() .
.


科目:初中数学 来源: 题型:
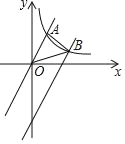
【题目】如图,已知直线y=![]() x与反比例函数y=
x与反比例函数y=![]() (x>0)的图象交于点A(2,m);将直线y=
(x>0)的图象交于点A(2,m);将直线y=![]() x向下平移后与反比例函数y=
x向下平移后与反比例函数y=![]() (x>0)的图象交于点B,且△AOB的面积为3.
(x>0)的图象交于点B,且△AOB的面积为3.
(1)求k的值;
(2)求平移后所得直线的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
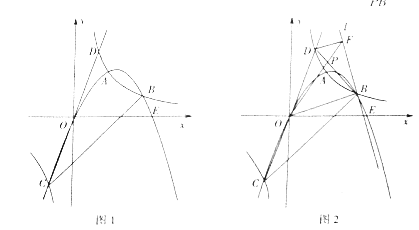
【题目】如图1所示,双曲线y=![]() (k≠0)与抛物线y=ax2+bx(a≠0)交于A、B、C三点,已知B(4,2),C(-2,-4),直线CO交双曲线于另一点D,抛物线与x轴交于另一点E.
(k≠0)与抛物线y=ax2+bx(a≠0)交于A、B、C三点,已知B(4,2),C(-2,-4),直线CO交双曲线于另一点D,抛物线与x轴交于另一点E.
(1)求双曲线和抛物线的解析式;
(2)在抛物线上是否存在点P,使得∠POE+∠BCD=90°?若存在,请求出满足条件的点P的坐标;若不存在,请说明理由;
(3)如图2所示,过点B作直线L⊥OB,过点D作DF⊥L于F,BD与OF交于点P,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
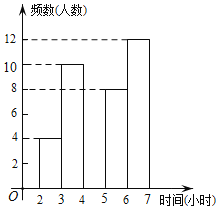
【题目】某中学为了了解学生每周在校体育锻炼时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) | 频数(人数) | 频率 |
2≤t<3 | 4 | 0.1 |
3≤t<4 | 10 | 0.25 |
4≤t<5 | a | 0.15 |
5≤t<6 | 8 | b |
6≤t<7 | 12 | 0.3 |
合计 | 40 | 1 |
(1)表中的a= ,b= ;
(2)请将频数分布直方图补全;
(3)若该校共有1200名学生,试估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BD为一条对角线,AD//BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.
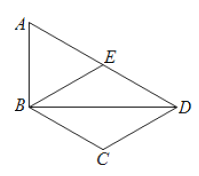
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,BC=1,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织初一师生春游,如果单独租用45座客车若干辆,刚好坐满;如果单独租用60座客车,可少租1辆,且余15个座位.
(1)求参加春游的人数;
(2)已知租用45座的客车日租金为每辆车250元, 60座的客车日租金为每辆300元,问租哪种客车更合算?省多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点O是原点,点A在数轴上,点A表示的数为-6,点B在原点的右侧,且OB=![]() OA,
OA,

(1)点B对应的数是_________,在数轴上标出点B。
(2)已知点P、点Q是数轴上的两个动点,点P从点A出发,以1个单位/秒的速度向右运动,同时点Q从点B出发,以3个单位/秒的速度向左运动;
①用含t的式子分别表示P、Q两点表示的数:P是__________;Q是____________;
②若点P和点Q经过t秒后在数轴上的点D处相遇,求出t的值和点D所表示的数;
③求经过几秒,点P与点Q分别到原点的距离相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(定义学习)
定义:如果四边形有一组对角为直角,那么我们称这样的四边形为“对直四边形”
(判断尝试)
在①梯形;②矩形:③菱形中,是“对直四边形”的是哪一个. (填序号)
(操作探究)
在菱形ABCD中,![]() 于点E,请在边AD和CD上各找一点F,使得以点A、E、C、F组成的四边形为“对直四边形”,画出示意图,并直接写出EF的长,
于点E,请在边AD和CD上各找一点F,使得以点A、E、C、F组成的四边形为“对直四边形”,画出示意图,并直接写出EF的长,

(实践应用)
某加工厂有一批四边形板材,形状如图所示,若AB=3米,AD=1米,![]()
![]()
.现根据客户要求,需将每张四边形板材进一步分割成两个等腰三角形板材和一个“对直四边形"板材,且这两个等腰三角形的腰长相等,要求材料充分利用无剩余.求分割后得到的等腰三角形的腰长,

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019杨家埠民俗文化灯会于正月初一至二十(2.5-2.24)在杨家埠民间艺术大观园举办,此前,杨家埠民俗文化灯会已经成功举办了四届,每年入园游客达百万人次,极大地丰富了市民群众的春节文化生活.为了了解今年的游客构成情况,抽取了其中1天的数据进行调研.当天接待![]() 地游客0.9万人,
地游客0.9万人,![]() 地游客2.4万人,
地游客2.4万人,![]() 地游客2.1万人,
地游客2.1万人,![]() 地游客0.1万人,
地游客0.1万人,![]() 地游客情况如图所示,其扇形圆心角为
地游客情况如图所示,其扇形圆心角为![]() .
.
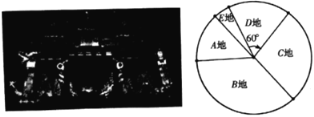
(1)抽到这一天当天的游客有多少人?
(2)当天A地游客占游客总数的百分比是多少?(精确到0.01%)
(3)当天C地游客在扇形统计图中的圆心角是多少度?(结果保留整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com