
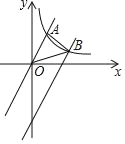
【题目】如图,已知直线y=![]() x与反比例函数y=
x与反比例函数y=![]() (x>0)的图象交于点A(2,m);将直线y=
(x>0)的图象交于点A(2,m);将直线y=![]() x向下平移后与反比例函数y=
x向下平移后与反比例函数y=![]() (x>0)的图象交于点B,且△AOB的面积为3.
(x>0)的图象交于点B,且△AOB的面积为3.
(1)求k的值;
(2)求平移后所得直线的函数表达式.
【答案】(1)k=6;(2)平移后所得直线的函数表达式为y=![]() x﹣3.
x﹣3.
【解析】分析:(1)先根据一次函数解析式求点A的坐标,再利用待定系数法求k的值;
(2)作辅助线AH,得AH=2,根据同底等高的两个三角形面积相等得:S△AOB=S△AOC=3,可得OC=3,写出C(0,-3),根据平行可设直线BC的函数表达式为y=![]() x+b,代入点C的坐标可得解析式.
x+b,代入点C的坐标可得解析式.
详解:(1)∵点A(2,m)在直线y=![]() x上,
x上,
∴m=![]() =3,则A(2,3);
=3,则A(2,3);
又点A(2,3)在反比例函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴3=![]() ,则k=6;
,则k=6;
(2)设平移后的直线与y轴交于点C,连接AC,过点A作AH⊥y轴于H,
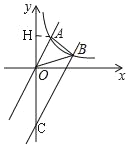
则AH=2,
∵BC∥OA,
∴S△AOB=S△AOC=3,
∴![]() OCAH=
OCAH=![]() OC2=3,
OC2=3,
则OC=3,
∵点C在y轴的负半轴上,
∴C(0,﹣3),
设直线BC的函数表达式为y=![]() x+b,
x+b,
∴将C(0,﹣3)代入得:b=﹣3,
∴平移后所得直线的函数表达式为y=![]() x﹣3.
x﹣3.


 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球20个,某学习小组做摸球实验,将球搅匀后从中随机摸出一个记下颜色,再把它放回口袋中,不断重复,如表是活动进行中的一组数据统计:
摸球的次数m | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数n | 58 | 96 | 116 | 295 | 484 | 601 |
摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
(1)请估计:当n很大时,摸到白球的频率将会接近________ ;
(2)假如你去摸一次,你摸到白球的概率是________,摸到黑球的概率是________;
(3)试估算口袋中黑球有________个,白球有________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线 y=kx+b(k≠0)过点 F(0,1),与抛物线 ![]() 相交于B、C 两点
相交于B、C 两点
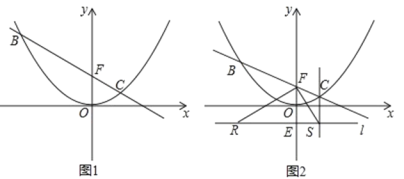
(1)如图 1,当点 C 的横坐标为 1 时,求直线 BC 的解析式;
(2)在(1)的条件下,点 M 是直线 BC 上一动点,过点 M 作 y 轴的平行线,与抛物线交于点 D, 是否存在这样的点 M,使得以 M、D、O、F 为顶点的四边形为平行四边形?若存在,求出点 M 的坐标;若不存在,请说明理由;
(3)如图 2,设 B(m,n)(m<0),过点 E(0,-1)的直线 l∥x 轴,BR⊥l 于 R,CS⊥l 于 S,连接 FR、FS.试判断△ RFS 的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】典典同学学完统计知识后,随机调查了她家所在辖区若干名居民的年龄,将调查数据绘制成如下扇形和条形统计图:
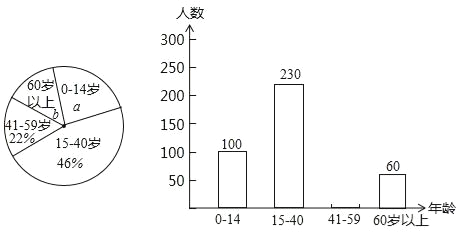
请根据以上不完整的统计图提供的信息,解答下列问题:
(1)扇形统计图中a= ,b= ;并补全条形统计图;
(2)若该辖区共有居民3500人,请估计年龄在0~14岁的居民的人数.
(3)一天,典典知道了辖区内60岁以上的部分老人参加了市级门球比赛,比赛的老人们分成甲、乙两组,典典很想知道甲乙两组的比赛结果,王大爷告诉说,甲组与乙组的得分和为110,甲组得分不低于乙组得分的1.5倍,甲组得分最少为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016湖北省孝感市)如图示我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan∠ADE的值为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强在某超市同时购买A,B两种商品共三次,仅有第一次超市将A,B两种商品同时按![]() 折价格出售,其余两次均按标价出售. 小强三次购买A,B商品的数量和费用如下表所示:
折价格出售,其余两次均按标价出售. 小强三次购买A,B商品的数量和费用如下表所示:
A商品的数量(个) | B商品的数量(个) | 购买总费用(元) | |
第一次购买 | 8 | 6 | 930 |
第二次购买 | 6 | 5 | 980 |
第三次购买 | 3 | 8 | 1040 |
(1)求 A,B商品的标价;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
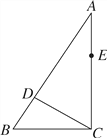
【题目】如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某餐厅中1张餐桌可坐6人,有以下两种摆放方式:
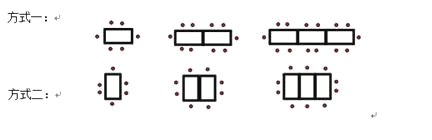
(1)对于方式一,4张桌子拼在一起可坐多少人?![]() 张桌子呢?对于方式二呢?
张桌子呢?对于方式二呢?
(2)该餐厅有40张这样的长方形桌子,按方式一每5张拼成一张大桌子,则40张桌子可拼成8张大桌子,共可坐多少人?按方式二呢?
(3)在(2)中,若改成每8张拼成一张大桌子,则共可坐多少人?
(4)一天中午,该餐厅来了98为顾客共同就餐,但餐厅中只有25张这样的长方形桌子可用,若你是这家餐厅的经理,你打算选择哪种方式来摆餐桌呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直角梯形ABCO中,∠AOC=90°,AB∥x轴,AB=6,若以O为原点,OA,OC所在直线为y轴和x轴建立如图所示直角坐标系,A(0,a),C(c,0)中a,c满足|a+c﹣10|+![]() =0
=0
(1)求出点A、B、C的坐标;
(2)如图2,若点M从点C出发,以2单位/秒的速度沿CO方向移动,点N从原点出发,以1单位/秒的速度沿OA方向移动,设M、N两点同时出发,且运动时间为t秒,当点N从点O运动到点A时,点M同时也停止运动,在它们的移动过程中,当2S△ABN≤S△BCM时,求t的取值范围:
(3)如图3,若点N是线段OA延长上的一动点,∠NCH=k∠OCH,∠CNQ=k∠BNQ,其中k>1,NQ∥CJ,求![]() 的值(结果用含k的式子表示).
的值(结果用含k的式子表示).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com