
【题目】已知直线 y=kx+b(k≠0)过点 F(0,1),与抛物线 ![]() 相交于B、C 两点
相交于B、C 两点
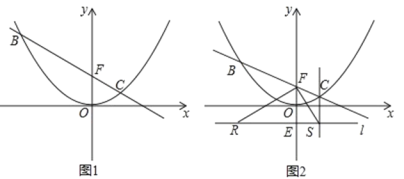
(1)如图 1,当点 C 的横坐标为 1 时,求直线 BC 的解析式;
(2)在(1)的条件下,点 M 是直线 BC 上一动点,过点 M 作 y 轴的平行线,与抛物线交于点 D, 是否存在这样的点 M,使得以 M、D、O、F 为顶点的四边形为平行四边形?若存在,求出点 M 的坐标;若不存在,请说明理由;
(3)如图 2,设 B(m,n)(m<0),过点 E(0,-1)的直线 l∥x 轴,BR⊥l 于 R,CS⊥l 于 S,连接 FR、FS.试判断△ RFS 的形状,并说明理由.
【答案】(1)![]() ;(2)存在;M点坐标为:(-3,
;(2)存在;M点坐标为:(-3,![]() ),
),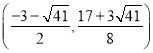 ,
,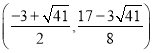 ;(3)△RFS是直角三角形;证明见详解.
;(3)△RFS是直角三角形;证明见详解.
【解析】
(1)首先求出C的坐标,然后由C、F两点用待定系数法求解析式即可;
(2)因为DM∥OF,要使以M、D、O、F为顶点的四边形为平行四边形,则DM=OF,设M(x,![]() ),则D(x,
),则D(x,![]() x2),表示出DM,分类讨论列方程求解;
x2),表示出DM,分类讨论列方程求解;
(3)根据勾股定理求出BR=BF,再由BR∥EF得到∠RFE=∠BFR,同理可得∠EFS=∠CFS,所以∠RFS=![]() ∠BFC=90°,所以△RFS是直角三角形.
∠BFC=90°,所以△RFS是直角三角形.
解:(1)因为点C在抛物线上,所以C(1,![]() ),
),
又∵直线BC过C、F两点,
故得方程组: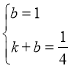
解之,得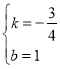 ,
,
所以直线BC的解析式为:![]() ;
;
(2)存在;理由如下:
要使以M、D、O、F为顶点的四边形为平行四边形,则MD=OF,如图1所示,
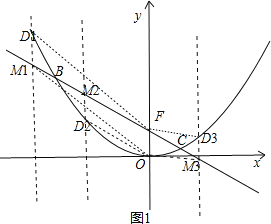
设M(x,![]() ),则D(x,
),则D(x,![]() x2),
x2),
∵MD∥y轴,
∴![]() ,
,
由MD=OF,可得:![]() ;
;
①当![]() 时,
时,
解得:x1=0(舍)或x1=-3,
所以M(-3,![]() );
);
②当![]() 时,
时,
解得:![]() ,
,
所以M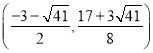 或M
或M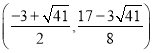 ,
,
综上所述,存在这样的点M,使以M、D、O、F为顶点的四边形为平行四边形,
M点坐标为:(-3,![]() ),
),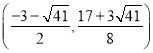 ,
,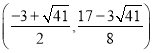 ;
;
(3)△RFS是直角三角形;理由如下:
过点F作FT⊥BR于点T,如图2所示,
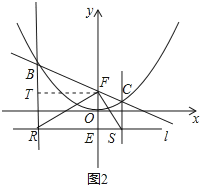
∵点B(m,n)在抛物线上,
∴m2=4n,
在Rt△BTF中,
![]()
![]()
![]()
![]() ,
,
∵n>0,
∴BF=n+1,
又∵BR=n+1,
∴BF=BR.
∴∠BRF=∠BFR,
又∵BR⊥l,EF⊥l,
∴BR∥EF,
∴∠BRF=∠RFE,
∴∠RFE=∠BFR,
同理可得∠EFS=∠CFS,
∴∠RFS=![]() ∠BFC=90°,
∠BFC=90°,
∴△RFS是直角三角形.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】【阅读理解】
若![]() ,
, ![]() ,
, ![]() 为数轴上三点,若点
为数轴上三点,若点![]() 到
到![]() 的距离是点
的距离是点![]() 到
到![]() 的距离的
的距离的![]() 倍,我们就称点
倍,我们就称点![]() 是
是![]() 的优点.例如,如图①,点
的优点.例如,如图①,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() .表示数
.表示数![]() 的点
的点![]() 到点
到点![]() 的距离是
的距离是![]() ,到点
,到点![]() 的距离是
的距离是![]() ,那么点
,那么点![]() 是
是![]() 的优点;又如,表示
的优点;又如,表示![]() 的点
的点![]() 到点
到点![]() 的距离是
的距离是![]() ,到点
,到点![]() 的距离是
的距离是![]() ,那么但点
,那么但点![]() 是
是![]() 的好点.
的好点.
【知识运用】
如图②,![]() 、
、![]() 为数轴上两点,点
为数轴上两点,点![]() 所表示的数为
所表示的数为![]() ,点
,点![]() 所表示的数为
所表示的数为![]() .
.
(![]() )数__________所表示的点是
)数__________所表示的点是![]() 的优点.
的优点.
(![]() )如图③,
)如图③,![]() ,
, ![]() 为数轴上两点,点
为数轴上两点,点![]() 所表示的数为
所表示的数为![]() ,点
,点![]() 所表示的数为
所表示的数为![]() .现有一只电子蚂蚁
.现有一只电子蚂蚁![]() 从点
从点![]() 出发,以
出发,以![]() 个单位每秒的速度向左运动,到达点
个单位每秒的速度向左运动,到达点![]() 停止.当
停止.当![]() 为何值时,
为何值时, ![]() 、
、![]() 和
和![]() 中恰有一个点为其余两点的好点?(请直接写出答案)
中恰有一个点为其余两点的好点?(请直接写出答案)


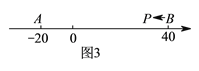
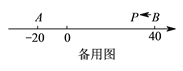
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:如果矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的覆盖矩形.点A,B,C的所有覆盖矩形中,面积最小的矩形称为点A,B,C的最优覆盖矩形.例如,下图中的矩形A1B1C1D1,A2B2C2D2,AB3C3D3都是点A,B,C的覆盖矩形,其中矩形AB3C3D3是点A,B,C的最优覆盖矩形.

(1)已知A(![]() 2,3),B(5,0),C(
2,3),B(5,0),C(![]() ,
, ![]() 2).
2).
①当![]() 时,点A,B,C的最优覆盖矩形的面积为 ;
时,点A,B,C的最优覆盖矩形的面积为 ;
②若点A,B,C的最优覆盖矩形的面积为40,则t的值为 ;
(2)已知点D(1,1),点E(![]() ,
, ![]() ),其中点E是函数
),其中点E是函数![]() 的图像上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
的图像上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成任务:
自相似图形
定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接EG,HF交于点O,易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形,且与原正方形相似,故正方形是自相似图形.
任务:
(1)图1中正方形ABCD分割成的四个小正方形中,每个正方形与原正方形的相似比为 ;
(2)如图2,已知△ABC中,∠ACB=90°,AC=4,BC=3,小明发现△ABC也是“自相似图形”,他的思路是:过点C作CD⊥AB于点D,则CD将△ABC分割成2个与它自己相似的小直角三角形.已知△ACD∽△ABC,则△ACD与△ABC的相似比为 ;
(3)现有一个矩形ABCD是自相似图形,其中长AD=a,宽AB=b(a>b).
请从下列A、B两题中任选一条作答:我选择 题.
A:①如图3﹣1,若将矩形ABCD纵向分割成两个全等矩形,且与原矩形都相似,则a= (用含b的式子表示);
②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形,且与原矩形都相似,则a= (用含n,b的式子表示);
B:①如图4﹣1,若将矩形ABCD先纵向分割出2个全等矩形,再将剩余的部分横向分割成3个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含b的式子表示);
②如图4﹣2,若将矩形ABCD先纵向分割出m个全等矩形,再将剩余的部分横向分割成n个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含m,n,b的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个三角形的第一条边为2a 5b ,第二条边比第一条边长3a 2b ,第三条边比第二条边短3a 。
(1)则第二条边的边长为 ,第三条边的边长为 ;
(2)用含a , b 的代数式表示这个三角形的周长,并化简;
(3)若a , b 满足 |a 4| (b 3)2 0,求这个三角形的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
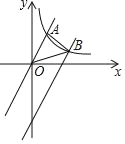
【题目】如图,已知直线y=![]() x与反比例函数y=
x与反比例函数y=![]() (x>0)的图象交于点A(2,m);将直线y=
(x>0)的图象交于点A(2,m);将直线y=![]() x向下平移后与反比例函数y=
x向下平移后与反比例函数y=![]() (x>0)的图象交于点B,且△AOB的面积为3.
(x>0)的图象交于点B,且△AOB的面积为3.
(1)求k的值;
(2)求平移后所得直线的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
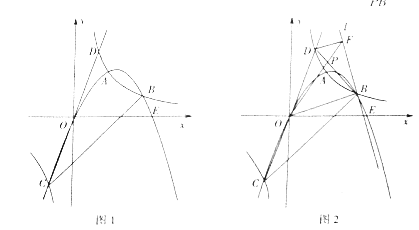
【题目】如图1所示,双曲线y=![]() (k≠0)与抛物线y=ax2+bx(a≠0)交于A、B、C三点,已知B(4,2),C(-2,-4),直线CO交双曲线于另一点D,抛物线与x轴交于另一点E.
(k≠0)与抛物线y=ax2+bx(a≠0)交于A、B、C三点,已知B(4,2),C(-2,-4),直线CO交双曲线于另一点D,抛物线与x轴交于另一点E.
(1)求双曲线和抛物线的解析式;
(2)在抛物线上是否存在点P,使得∠POE+∠BCD=90°?若存在,请求出满足条件的点P的坐标;若不存在,请说明理由;
(3)如图2所示,过点B作直线L⊥OB,过点D作DF⊥L于F,BD与OF交于点P,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com