
【题目】某餐厅中1张餐桌可坐6人,有以下两种摆放方式:
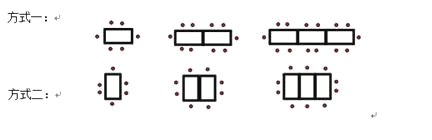
(1)对于方式一,4张桌子拼在一起可坐多少人?![]() 张桌子呢?对于方式二呢?
张桌子呢?对于方式二呢?
(2)该餐厅有40张这样的长方形桌子,按方式一每5张拼成一张大桌子,则40张桌子可拼成8张大桌子,共可坐多少人?按方式二呢?
(3)在(2)中,若改成每8张拼成一张大桌子,则共可坐多少人?
(4)一天中午,该餐厅来了98为顾客共同就餐,但餐厅中只有25张这样的长方形桌子可用,若你是这家餐厅的经理,你打算选择哪种方式来摆餐桌呢?
【答案】(1)方式一:18人;4n+2 ;方式二:12人; 2n+4
(2)方式一:176人;方式二:112人
(3)方式一170人 方式二 100人
(4)打算用第一种摆放方式来摆放餐桌。
【解析】
(1)对于方式一,4张桌子拼在一起可坐18人,n张桌子可以坐(4n+2)人,
对于方式二,4张桌子拼在一起可坐12人,n张桌子可以坐(2n+4)人,
(2)该餐厅有40张这样的长方形桌子,按方式一每5张拼成一张大桌子,则40张桌子可拼成8张大桌子,共可坐176人;按方式二每5张拼成一张大桌子,则40张桌子可拼成8张大桌子,共可坐112人,
(3)若改成每8张拼成一张大桌子,按方式一共可坐170人;按方式二共可坐100人.
(4)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌, 则选择方式一来摆放餐桌,每5张拼成一张大桌子,则25张桌子可拼成5张大桌子.
解:(1)方式一,4张桌子拼在一起可坐18人,n张桌子可以坐6+4(n-1)=(4n+2)人,对于方式二,4张桌子拼在一起可坐12人,n张桌子可以坐6+2(n-1)=(2n+4)人,
(2)餐厅有40张这样的长方形桌子,按方式一每5张拼成一张大桌子,则40张桌子可拼成8张大桌子,共可坐176人;按方式二每5张拼成一张大桌子,则40张桌子可拼成8张大桌子,共可坐112人,
(3)若改成每8张拼成一张大桌子,按方式一共可坐170人;按方式二共可坐100人.
(4)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌, 则选择方式一来摆放餐桌,每5张拼成一张大桌子,则25张桌子可拼成5张大桌子,


科目:初中数学 来源: 题型:
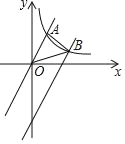
【题目】如图,已知直线y=![]() x与反比例函数y=
x与反比例函数y=![]() (x>0)的图象交于点A(2,m);将直线y=
(x>0)的图象交于点A(2,m);将直线y=![]() x向下平移后与反比例函数y=
x向下平移后与反比例函数y=![]() (x>0)的图象交于点B,且△AOB的面积为3.
(x>0)的图象交于点B,且△AOB的面积为3.
(1)求k的值;
(2)求平移后所得直线的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.

(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点C在线段AB上,点M,N分别在线段AC与线段BC上,且AM=2MC,BN=2NC.
![]()
(1)若AC=9,BC=6,求线段MN的长;
(2)若MN=5,求线段AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD 中,边CD 5 ,对角线 AC 8 , DB 6.
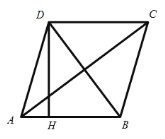
(1)求证:四边形 ABCD 是菱形;
(2)过点 D 作 DH AB 于点 H ,若点 P 是线段 AC 上的一个动点,求 PH PB 的最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
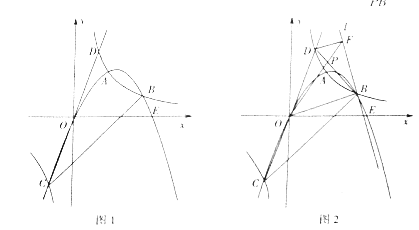
【题目】如图1所示,双曲线y=![]() (k≠0)与抛物线y=ax2+bx(a≠0)交于A、B、C三点,已知B(4,2),C(-2,-4),直线CO交双曲线于另一点D,抛物线与x轴交于另一点E.
(k≠0)与抛物线y=ax2+bx(a≠0)交于A、B、C三点,已知B(4,2),C(-2,-4),直线CO交双曲线于另一点D,抛物线与x轴交于另一点E.
(1)求双曲线和抛物线的解析式;
(2)在抛物线上是否存在点P,使得∠POE+∠BCD=90°?若存在,请求出满足条件的点P的坐标;若不存在,请说明理由;
(3)如图2所示,过点B作直线L⊥OB,过点D作DF⊥L于F,BD与OF交于点P,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
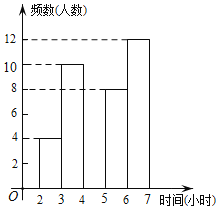
【题目】某中学为了了解学生每周在校体育锻炼时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) | 频数(人数) | 频率 |
2≤t<3 | 4 | 0.1 |
3≤t<4 | 10 | 0.25 |
4≤t<5 | a | 0.15 |
5≤t<6 | 8 | b |
6≤t<7 | 12 | 0.3 |
合计 | 40 | 1 |
(1)表中的a= ,b= ;
(2)请将频数分布直方图补全;
(3)若该校共有1200名学生,试估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(定义学习)
定义:如果四边形有一组对角为直角,那么我们称这样的四边形为“对直四边形”
(判断尝试)
在①梯形;②矩形:③菱形中,是“对直四边形”的是哪一个. (填序号)
(操作探究)
在菱形ABCD中,![]() 于点E,请在边AD和CD上各找一点F,使得以点A、E、C、F组成的四边形为“对直四边形”,画出示意图,并直接写出EF的长,
于点E,请在边AD和CD上各找一点F,使得以点A、E、C、F组成的四边形为“对直四边形”,画出示意图,并直接写出EF的长,

(实践应用)
某加工厂有一批四边形板材,形状如图所示,若AB=3米,AD=1米,![]()
![]()
.现根据客户要求,需将每张四边形板材进一步分割成两个等腰三角形板材和一个“对直四边形"板材,且这两个等腰三角形的腰长相等,要求材料充分利用无剩余.求分割后得到的等腰三角形的腰长,

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com