
【题目】如图,已知点C在线段AB上,点M,N分别在线段AC与线段BC上,且AM=2MC,BN=2NC.
![]()
(1)若AC=9,BC=6,求线段MN的长;
(2)若MN=5,求线段AB的长.
【答案】(1)5;(2)15
【解析】
(1)首先由AM=2MC,BN=2NC可得AC=3MC,BC=3NC,然后根据AC=9和BC=6可求出MC和NC,最后根据MN=MC+NC可得答案;
(2)由(1)可知AC=3MC,BC=3NC,两式相加可得AB=3(MC+NC)=3MN,即可得出答案.
解:(1)∵AM=2MC,BN=2NC
∴AC=3MC,BC=3NC,
∵AC=9,BC=6
∴MC=![]() AC=3,NC=
AC=3,NC=![]() BC=2
BC=2
∴MN=MC+NC=3+2=5
(2)由(1)可知AC=3MC①,BC=3NC②,
①+②得:AC+BC=3MC+3NC
即AB=3(MC+NC)=3MN
∵MN=5
∴AB=3×5=15


科目:初中数学 来源: 题型:
【题目】“邮扬新干线”是指从高邮站开往扬州站的公交车,中途只停靠江都站,现甲、乙、丙3名不相识的乘客同时从高邮站上车。
(1)求甲、乙、丙三名乘客在同一个站下车的概率;
(2)求甲、乙、丙三名乘客中至少有一人在江都站下车的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016湖北省孝感市)如图示我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan∠ADE的值为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
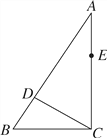
【题目】如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
查看答案和解析>>
科目:初中数学 来源: 题型:
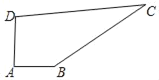
【题目】芬芳园有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m,求草皮的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某餐厅中1张餐桌可坐6人,有以下两种摆放方式:
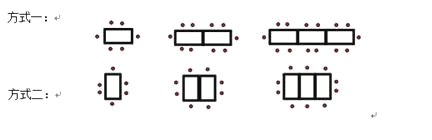
(1)对于方式一,4张桌子拼在一起可坐多少人?![]() 张桌子呢?对于方式二呢?
张桌子呢?对于方式二呢?
(2)该餐厅有40张这样的长方形桌子,按方式一每5张拼成一张大桌子,则40张桌子可拼成8张大桌子,共可坐多少人?按方式二呢?
(3)在(2)中,若改成每8张拼成一张大桌子,则共可坐多少人?
(4)一天中午,该餐厅来了98为顾客共同就餐,但餐厅中只有25张这样的长方形桌子可用,若你是这家餐厅的经理,你打算选择哪种方式来摆餐桌呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
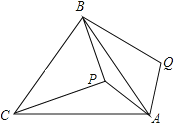
【题目】(2016四川省达州市)如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,连接BQ.若PA=6,PB=8,PC=10,则四边形APBQ的面积为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中考前各校初三学生都要进行体育测试,某次中考体育测试设有A、B两处考点,甲、乙、丙三名学生各自随机选择其中的一处进行中考体育测试,请用表格或树状图分析:
(1)求甲、乙、丙三名学生在同一处进行体育测试的概率;
(2)求甲、乙、丙三名学生中至少有两人在B处进行体育测试的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列说法:
①2+3x-5x3是三次四项式;②﹣a一定在原点的左边.③![]() 是分数,它是有理数;④有最大的负整数,没有最大的正整数;⑤近似数5.60所表示的准确数x的范围是:5.55≤x<5.65.其中错误的个数是( )
是分数,它是有理数;④有最大的负整数,没有最大的正整数;⑤近似数5.60所表示的准确数x的范围是:5.55≤x<5.65.其中错误的个数是( )
A.2B.3C.4D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com