[题目]“邮扬新干线是指从高邮站开往扬州站的公交车.中途只停靠江都站.现甲.乙.丙3名不相识的乘客同时从高邮站上车.(1)求甲.乙.丙三名乘客在同一个站下车的概率,(2)求甲.乙.丙三名乘客中至少有一人在江都站下车的概率. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】“邮扬新干线”是指从高邮站开往扬州站的公交车，中途只停靠江都站，现甲、乙、丙3名不相识的乘客同时从高邮站上车。

（1）求甲、乙、丙三名乘客在同一个站下车的概率；

（2）求甲、乙、丙三名乘客中至少有一人在江都站下车的概率。

【答案】（1）；（2）

【解析】试题分析：（1）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与甲、乙、丙三名旅客在同一个站下车的情况，再利用概率公式即可求得答案；

（2）由（1）可求得甲、乙、丙三名旅客中至少有一人在江都站下车的有7种情况；然后利用概率公式求解即可求得答案．

试题解析：解：（1）画树状图得：

∵共有8种等可能的结果，甲、乙、丙三名旅客在同一个站下车的有2种情况，∴甲、乙、丙三名旅客在同一个站下车的概率为： =；

（2）∵甲、乙、丙三名旅客中至少有一人在江都站下车的有7种情况；

∴甲、乙、丙三名旅客中至少有一人在江都站下车的概率为：．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】小方家住户型呈长方形，平面图如下(单位：米)，现准备铺设地面，三间卧室铺设木地板，其它区城铺设地砖.

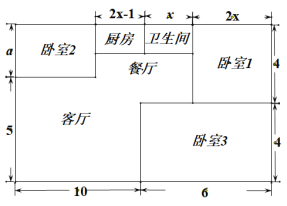
(1)求a的值.

(2)铺设地面需要木地板和地砖各多少平方米(用含的代数式表示)？

(3)按市场价格，木地板单价为300元/平方米，地砖单价为100元/平方米，装修公司有两种活动方案，如表：

活动方案	木地板价格	地砖价格	总安装费
A	8折	8.5折	2000元
B	9折	8.5折	免收

已知卧室2的面积是21平方米，则小方家应选择哪种活动，使铺设地面的总费用（包括材料费及安装费）更低？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，直线y＝﹣x+与x轴、y轴分别交于点A、B，在坐标轴上找点P，使△ABP为等腰三角形，则点P的个数为（）

A. 2B. 4C. 6D. 8

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】在直角中，，，AD，CE分别是和的平分线，AD，CE相交于点F．

求的度数；

判断FE与FD之间的数量关系，并证明你的结论．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】对于三个数a，b，c，用M{a，b，c}表示这三个数的平均数，用min{a，b，c}表示这三个数中最小的数．例如：M{－1，2，3}＝，min{－1，2，3}＝－1，如果M{3，2x＋1，4x－1}＝min{2，－x＋3，5x}，那么x＝____________.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在△ABC中，∠ ACB=115O，BD=BC,AE=AC. 则∠ECD的度数为_________.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】在平面直角坐标系xOy中，对于任意三点A，B，C，给出如下定义：如果矩形的任何一条边均与某条坐标轴平行，且A，B，C三点都在矩形的内部或边界上，则称该矩形为点A，B，C的覆盖矩形．点A，B，C的所有覆盖矩形中，面积最小的矩形称为点A，B，C的最优覆盖矩形．例如，下图中的矩形A1B1C1D1，A2B2C2D2，AB3C3D3都是点A，B，C的覆盖矩形，其中矩形AB3C3D3是点A，B，C的最优覆盖矩形．