
【题目】(2016湖北省孝感市)如图示我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan∠ADE的值为_________.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+
x+![]() 与x轴、y轴分别交于点A、B,在坐标轴上找点P,使△ABP为等腰三角形,则点P的个数为( )
与x轴、y轴分别交于点A、B,在坐标轴上找点P,使△ABP为等腰三角形,则点P的个数为( )

A. 2B. 4C. 6D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:如果矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的覆盖矩形.点A,B,C的所有覆盖矩形中,面积最小的矩形称为点A,B,C的最优覆盖矩形.例如,下图中的矩形A1B1C1D1,A2B2C2D2,AB3C3D3都是点A,B,C的覆盖矩形,其中矩形AB3C3D3是点A,B,C的最优覆盖矩形.

(1)已知A(![]() 2,3),B(5,0),C(
2,3),B(5,0),C(![]() ,
, ![]() 2).
2).
①当![]() 时,点A,B,C的最优覆盖矩形的面积为 ;
时,点A,B,C的最优覆盖矩形的面积为 ;
②若点A,B,C的最优覆盖矩形的面积为40,则t的值为 ;
(2)已知点D(1,1),点E(![]() ,
, ![]() ),其中点E是函数
),其中点E是函数![]() 的图像上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
的图像上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个三角形的第一条边为2a 5b ,第二条边比第一条边长3a 2b ,第三条边比第二条边短3a 。
(1)则第二条边的边长为 ,第三条边的边长为 ;
(2)用含a , b 的代数式表示这个三角形的周长,并化简;
(3)若a , b 满足 |a 4| (b 3)2 0,求这个三角形的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.

(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
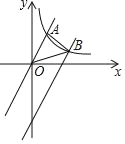
【题目】如图,已知直线y=![]() x与反比例函数y=
x与反比例函数y=![]() (x>0)的图象交于点A(2,m);将直线y=
(x>0)的图象交于点A(2,m);将直线y=![]() x向下平移后与反比例函数y=
x向下平移后与反比例函数y=![]() (x>0)的图象交于点B,且△AOB的面积为3.
(x>0)的图象交于点B,且△AOB的面积为3.
(1)求k的值;
(2)求平移后所得直线的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是⊙O的内接三角形,AB为⊙O的直径,OD⊥AB于点O,且∠ODC=2∠A.
(1)求证:CD是⊙O的切线;
(2)若AB=6,tan∠A=![]() ,求CD的长.
,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点C在线段AB上,点M,N分别在线段AC与线段BC上,且AM=2MC,BN=2NC.
![]()
(1)若AC=9,BC=6,求线段MN的长;
(2)若MN=5,求线段AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BD为一条对角线,AD//BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.
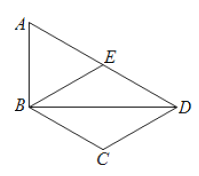
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,BC=1,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com