
【题目】如图,已知△ABC是⊙O的内接三角形,AB为⊙O的直径,OD⊥AB于点O,且∠ODC=2∠A.
(1)求证:CD是⊙O的切线;
(2)若AB=6,tan∠A=![]() ,求CD的长.
,求CD的长.

【答案】(1)见解析;(2)4.
【解析】分析:(1)连接OC,求出∠ODC=∠B,求出∠OCD=90°,根据切线的判定得出即可;
(2)过点C作CH⊥AB于点H,解直角三角形求出BC,解直角三角形求出CH和BH,证Rt△DOC∽Rt△OCH,得出比例式,即可求出答案.
(1)证明:连接OC,
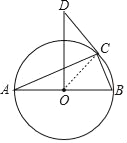
∵OA=OC,
∴∠A=∠ACO,
∴∠BOC=2∠A,
又∵∠ODC=2∠A,
∴∠ODC=∠BOC,
∵OD⊥AB,即∠BOC+∠COD=90°,
∴∠ODC+∠COD=90°,
∴∠OCD=90°,
即CD⊥OC,
又∵OC是⊙O的半径,
∴CD是⊙O的切线;
(2)如图,过点C作CH⊥AB于点H,
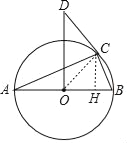
∵AB为⊙O的直径,点C在⊙O上,
∴∠ACB=90°,
又∵∠CBH=∠ABC,
∴∠BCH=∠A,
在Rt△ABC中,AB=6,tan∠A=![]() ,
,
设BC=x,则AC=3x,由勾股定理得:x2+(3x)2=62,
解得:x2=![]() ,
,
即BC2=![]() ,
,
又在Rt△BCH中,tan∠BCH=![]() ,
,
BH2+CH2=BC2,
即BH2+(3BH)2=![]() ,
,
解得:BH=![]() CH=
CH=![]() ,
,
∵OB=OC=3,
∴OH=![]() ,
,
又∵Rt△DOC∽Rt△OCH,
∴![]() ,
,
则CD=![]() =3×
=3×![]() ÷
÷![]() =4.
=4.


科目:初中数学 来源: 题型:
【题目】二次函数 y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线 x=1,则下列四个结论:①c>0; ②2a+b=0; ③b2-4ac>0; ④a-b+c>0;正确的是_____.
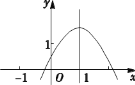
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设![]() =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是![]() 时,求AB的长.
时,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016湖北省孝感市)如图示我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan∠ADE的值为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在OA,OC上
(1)给出以下条件;①OB=OD,②∠1=∠2,③OE=OF,请你从中选取两个条件证明△BEO≌△DFO;
(2)在(1)条件中你所选条件的前提下,添加AE=CF,求证:四边形ABCD是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
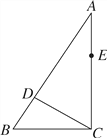
【题目】如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
查看答案和解析>>
科目:初中数学 来源: 题型:
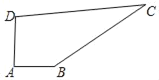
【题目】芬芳园有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m,求草皮的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
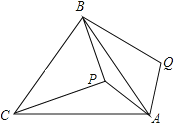
【题目】(2016四川省达州市)如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,连接BQ.若PA=6,PB=8,PC=10,则四边形APBQ的面积为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=BC,直线,MN经过点C,且AD⊥MN于点D,BE⊥MN于点E。
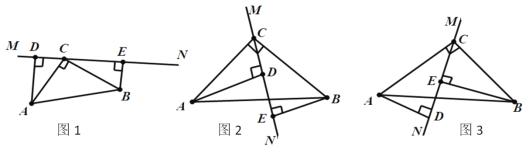
(1)当直线MN绕点C旋转到如图1的位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到如图2的位置时,求证:DE=AD-BE;
(3)当直线MN绕点C旋转到如图3的位置时,线段DE、AD、BE之间又有什么样的数量关系?请你写出这个数量关系,并证明
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com