Question

【题目】如图，在ABCD中，E是BC的中点，连接AE并延长交DC的延长线于点F．

（1）求证：AB=CF；

（2）连接DE，若AD=2AB，求证：DE⊥AF．

Answer 1

【答案】（1）根据平行四边形的性质可得AB∥CD，AB=CD，根据平行线的性质可得∠B=∠BCF，由E是BC的中点可得BE=CE，再结合对顶角相等可证得△ABE≌△FCE，问题得证；

（2）由AB=CD，AB=CF结合AD=2AB可证得AD=DF，再根据等腰三角形的性质即可作出判断.

【解析】试题分析：（1）由在ABCD中，E是BC的中点，利用ASA，即可判定△ABE≌△FCE，继而证得结论；（2）由AD=2AB，AB=FC=CD，可得AD=DF，又由△ABE≌△FCE，可得AE=EF，然后利用三线合一，证得结论．

试题解析：（1）∵四边形ABCD是平行四边形， ∴AB∥DF， ∴∠ABE=∠FCE， ∵E为BC中点， ∴BE=CE，

在△ABE与△FCE中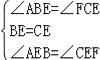，， ∴△ABE≌△FCE（ASA）， ∴AB=FC；

（2）∵AD=2AB，AB=FC=CD， ∴AD=DF， ∵△ABE≌△FCE， ∴AE=EF， ∴DE⊥AF．