
【题目】如图,四边形ABCD是平行四边形,E、F是对角线AC上的两点,∠1=∠2.

(1)求证:AE=CF;
(2)求证:四边形EBFD是平行四边形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】(1)通过证明△ADE≌△CBF,由全等三角的对应边相等证得AE=CF。
(2)根据平行四边形的判定定理:对边平行且相等的四边形是平行四边形证得结论。
证明:(1)如图:∵四边形ABCD是平行四边形,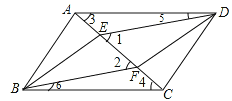
∴AD=BC,AD∥BC,∠3=∠4。
∵∠1=∠3+∠5,∠2=∠4+∠6,
∴∠1=∠2。
∴∠5=∠6。
∵在△ADE与△CBF中,∠3=∠4,AD=BC,∠5=∠6,
∴△ADE≌△CBF(ASA)。
∴AE=CF。
(2)∵∠1=∠2,∴DE∥BF。
又∵由(1)知△ADE≌△CBF,
∴DE=BF。
∴四边形EBFD是平行四边形.
“点睛”本题考查了平行四边形的判定和性质,全等三角形的判定和性质,灵活运用平行四边形的判定定理是解题关键.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的对称轴是直线
的对称轴是直线![]() .
.
(1)求抛物线的表达式;
(2)点![]() ,
, ![]() 在抛物线上,若
在抛物线上,若![]() ,请直接写出
,请直接写出![]() 的取值范围;
的取值范围;
(3)设点![]() 为抛物线上的一个动点,当
为抛物线上的一个动点,当![]() 时,点
时,点![]() 关于
关于![]() 轴的对称点都在直线
轴的对称点都在直线![]() 的上方,求
的上方,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列已知条件,能唯一画出△ABC的是( )
A.AB=6,BC=3,AC=9B.AB=5,BC=4,∠A=30°
C.∠C=90°,AB=6D.∠A=60°,∠B=45°,AB=4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.

(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市举行的中学生春季田径运动会上,参加男子跳高的15名运动员的成绩如下表所示:
成绩(m) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
人数 | 1 | 2 | 4 | 3 | 3 | 2 |
这些运动员跳高成绩的中位数和众数分别是( )
A.1.70,1.65
B.1.70,1.70
C.1.65,1.70
D.3,4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据表格估计一元二次方程x2+2x﹣4=0的一个解的范围在( )
x | ﹣1 | 0 | 1 | 2 | 3 |
x2+2x﹣4 | ﹣5 | ﹣4 | ﹣1 | 4 | 11 |
A.﹣1<x<0
B.0<x<1
C.1<x<2
D.2<x<3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com