
【题目】如图,已知点O是原点,点A在数轴上,点A表示的数为-6,点B在原点的右侧,且OB=![]() OA,
OA,

(1)点B对应的数是_________,在数轴上标出点B。
(2)已知点P、点Q是数轴上的两个动点,点P从点A出发,以1个单位/秒的速度向右运动,同时点Q从点B出发,以3个单位/秒的速度向左运动;
①用含t的式子分别表示P、Q两点表示的数:P是__________;Q是____________;
②若点P和点Q经过t秒后在数轴上的点D处相遇,求出t的值和点D所表示的数;
③求经过几秒,点P与点Q分别到原点的距离相等?
【答案】(1)8;数轴表示见解析;
(2)①-6+t; 8-3t;②t=![]() ;点D所表示的数是-2.5;③
;点D所表示的数是-2.5;③![]() 秒或1秒.
秒或1秒.
【解析】
(1)求出OB的长度即可;
(2)①表示出P的路程和Q的路程,根据左减右加即可表示出P、 Q的数;
②令P、 Q的数相等即可列出方程,解方程即可;
③表示出OP、OQ的长度,根据相等列出绝对值方程,解出即可.
(1)∵点A表示的数为-6
∴OA=6
∵OB=![]() OA
OA
∴OB=8
∵点B在原点的右侧
∴点B对应的数是8,数轴表示如图所示
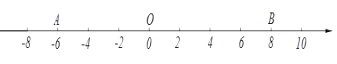
(2)①∵P的路程为t,Q的路程为3t
∴P是-6+t;Q是8-3t
②∵点P和点Q经过t秒后在数轴上的点D处相遇
∴-6+t=8-3t
∴t=![]()
∴点D所表示的数=-6+![]() =-2.5
=-2.5
③∵P是-6+t;Q是8-3t
∴OP=![]() ,OQ=
,OQ=![]()
∵点P与点Q分别到原点的距离相等
∴![]() =
=![]()
∴-6+t=8-3t或-6+t=3t-8
∴t=![]() 或t=1.
或t=1.
∴经过![]() 秒或1秒,点P与点Q分别到原点的距离相等.
秒或1秒,点P与点Q分别到原点的距离相等.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
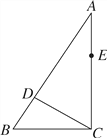
【题目】如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中考前各校初三学生都要进行体育测试,某次中考体育测试设有A、B两处考点,甲、乙、丙三名学生各自随机选择其中的一处进行中考体育测试,请用表格或树状图分析:
(1)求甲、乙、丙三名学生在同一处进行体育测试的概率;
(2)求甲、乙、丙三名学生中至少有两人在B处进行体育测试的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直角梯形ABCO中,∠AOC=90°,AB∥x轴,AB=6,若以O为原点,OA,OC所在直线为y轴和x轴建立如图所示直角坐标系,A(0,a),C(c,0)中a,c满足|a+c﹣10|+![]() =0
=0
(1)求出点A、B、C的坐标;
(2)如图2,若点M从点C出发,以2单位/秒的速度沿CO方向移动,点N从原点出发,以1单位/秒的速度沿OA方向移动,设M、N两点同时出发,且运动时间为t秒,当点N从点O运动到点A时,点M同时也停止运动,在它们的移动过程中,当2S△ABN≤S△BCM时,求t的取值范围:
(3)如图3,若点N是线段OA延长上的一动点,∠NCH=k∠OCH,∠CNQ=k∠BNQ,其中k>1,NQ∥CJ,求![]() 的值(结果用含k的式子表示).
的值(结果用含k的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=BC,直线,MN经过点C,且AD⊥MN于点D,BE⊥MN于点E。
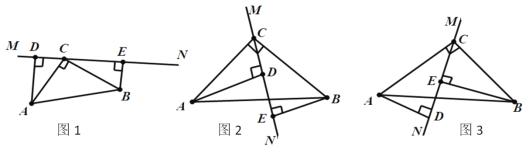
(1)当直线MN绕点C旋转到如图1的位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到如图2的位置时,求证:DE=AD-BE;
(3)当直线MN绕点C旋转到如图3的位置时,线段DE、AD、BE之间又有什么样的数量关系?请你写出这个数量关系,并证明
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某餐厅中,一张桌子可坐6人,有如图所示的两种摆放方式:

(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌.若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列说法:
①2+3x-5x3是三次四项式;②﹣a一定在原点的左边.③![]() 是分数,它是有理数;④有最大的负整数,没有最大的正整数;⑤近似数5.60所表示的准确数x的范围是:5.55≤x<5.65.其中错误的个数是( )
是分数,它是有理数;④有最大的负整数,没有最大的正整数;⑤近似数5.60所表示的准确数x的范围是:5.55≤x<5.65.其中错误的个数是( )
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD是正方形,AB=4,点G在BC边上,BG=3,DE⊥AG于点E,BF⊥AG于点F.
(1)求BF和DE的长;
(2)如图2,连接DF、CE,探究并证明线段DF与CE的数量关系与位置关系.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com