
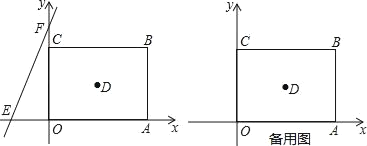
【题目】如图,在平面直角坐标系中,正方形OABC的边长为a.直线y=bx+c交x轴于E,交y轴于F,且a、b、c分别满足﹣(a﹣4)2≥0,c=![]() +8.
+8.
(1)求直线y=bx+c的解析式并直接写出正方形OABC的对角线的交点D的坐标;
(2)直线y=bx+c沿x轴正方向以每秒移动1个单位长度的速度平移,设平移的时间为t秒,问是否存在t的值,使直线EF平分正方形OABC的面积?若存在,请求出t的值;若不存在,请说明理由;
(3)点P为正方形OABC的对角线AC上的动点(端点A、C除外),PM⊥PO,交直线AB于M,求![]() 的值.
的值.
【答案】(1)y=2x+8,D(2,2);(2)存在,5;(3)![]() .
.
【解析】
试题(1)利用非负数的性质求出a,b,c的值,进而确定出直线y=bx+c,得到正方形的边长,即可确定出D坐标;
(2)存在,理由为:对于直线y=2x+8,令y=0求出x的值,确定出E坐标,根据题意得:当直线EF平移到过D点时正好平分正方形AOBC的面积,设平移后的直线方程为y=2x+t,将D坐标代入求出b的值,确定出平移后直线解析式,进而确定出此直线与x轴的交点,从而求出平移距离,得到t的值;
过P点作PQ∥OA,PH∥CO,交CO、AB于N、Q,交CB、OA于G、H,利用同角的余角相等得到一对角相等,再由一对直角相等,利用角平分线定理得到PH=PQ,利用AAS得到三角形OPH与三角形MPQ全等,得到OH=QM,根据四边形CNPG为正方形,得到PG=BQ=CN,由三角形CGP为等腰直角三角形得到CP=![]() GP=
GP=![]() BM,即可求出所求式子的值.
BM,即可求出所求式子的值.
试题解析:(1)∵-(a-4)2≥0,![]() ,
,
∴a=4,b=2,c=8,
∴直线y=bx+c的解析式为:y=2x+8,
∵正方形OABC的对角线的交点D,且正方形边长为4,
∴D(2,2);
(2)存在,理由为:
对于直线y=2x+8,
当y=0时,x=-4,
∴E点的坐标为(-4,0),
根据题意得:当直线EF平移到过D点时正好平分正方形AOBC的面积,
设平移后的直线为y=2x+t,
代入D点坐标(2,2),
得:2=4+t,即t=-2,
∴平移后的直线方程为y=2x-2,
令y=0,得到x=1,
∴此时直线和x轴的交点坐标为(1,0),平移的距离为1-(-4)=5,
则t=5秒;
(3)过P点作PQ∥OA,PH∥CO,交CO、AB于N、Q,交CB、OA于G、H,
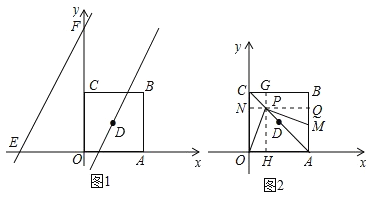
∵∠OPM=∠HPQ=90°,
∴∠OPH+∠HPM=90°,∠HPM+∠MPQ=90°,
∴∠OPH=∠MPQ,
∵AC为∠BAO平分线,且PH⊥OA,PQ⊥AB,
∴PH=PQ,
在△OPH和△MPQ中,
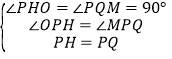 ,
,
∴△OPH≌△MPQ(AAS),
∴OH=QM,
∵四边形CNPG为正方形,
∴PG=BQ=CN,
∴CP=![]() PG=
PG=![]() BM,
BM,
即![]() .
.


科目:初中数学 来源: 题型:
【题目】某校组织初一师生春游,如果单独租用45座客车若干辆,刚好坐满;如果单独租用60座客车,可少租1辆,且余15个座位.
(1)求参加春游的人数;
(2)已知租用45座的客车日租金为每辆车250元, 60座的客车日租金为每辆300元,问租哪种客车更合算?省多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图,某住宅小区在施工过程中留下了一块空地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问用该草坪铺满这块空地共需花费多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湖南省作为全国第三批启动高考综合改革的省市之一,从2018年秋季入学的高中一年级学生开始实施高考综合改革.深化高考综合改革,承载着广大考生的美好期盼,事关千家万户的切身利益,社会关注度高.为了了解我市某小区居民对此政策的关注程度,某数学兴趣小组随机采访了该小区部分居民,根据采访情况制作了如下统计图表:
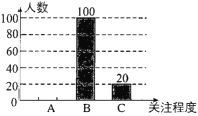
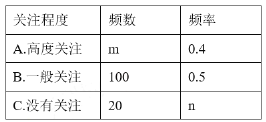
(1)根据上述统计图表,可得此次采访的人数为___________,m=___________,n=___________.
(2)根据以上信息补全图中的条形统计图.
(3)请估计在该小区1500名居民中,高度关注新高考政策的有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019杨家埠民俗文化灯会于正月初一至二十(2.5-2.24)在杨家埠民间艺术大观园举办,此前,杨家埠民俗文化灯会已经成功举办了四届,每年入园游客达百万人次,极大地丰富了市民群众的春节文化生活.为了了解今年的游客构成情况,抽取了其中1天的数据进行调研.当天接待![]() 地游客0.9万人,
地游客0.9万人,![]() 地游客2.4万人,
地游客2.4万人,![]() 地游客2.1万人,
地游客2.1万人,![]() 地游客0.1万人,
地游客0.1万人,![]() 地游客情况如图所示,其扇形圆心角为
地游客情况如图所示,其扇形圆心角为![]() .
.
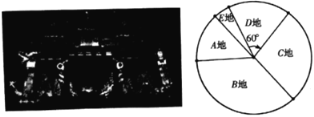
(1)抽到这一天当天的游客有多少人?
(2)当天A地游客占游客总数的百分比是多少?(精确到0.01%)
(3)当天C地游客在扇形统计图中的圆心角是多少度?(结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆出租车从甲地出发,在一条东西走向的街道上往返行驶,每次行驶的路程(记向东为正),记录如下表(![]() ,单位:
,单位:![]() ):
):
第1次 | 第2次 | 第3次 | 第4次 |
|
|
|
|
(1)说出这辆出租车每次行驶的方向.
(2)这辆出租车共行驶了多少路程?
查看答案和解析>>
科目:初中数学 来源: 题型:
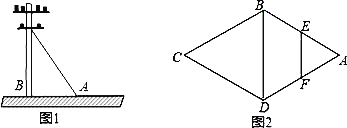
【题目】(1)如图1,要从电线杆离地面5m处向地面拉一条钢索,若地面钢索固定点A到电线杆底部B的距离为2m,求钢索的长度.
(2)如图2,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点,若EF=2,求菱形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一只甲虫在5×5的方格(每小格边长为1个单位长度)上沿着网格线运动,它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从D到C记为:D→C(-1,+2)第一个数表示左右方向,第二个数表示上下方向.
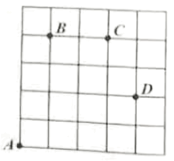
(1)图中A→C可以记为( , )
(2)图中D→ 可以记为(-4,-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】事业单位人员编制连进必考,现一事业单位需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方而进行量化考核.甲、乙、丙各项得分如下表:
笔试 | 面试 | 体能 | |
甲 | 84 | 80 | 88 |
乙 | 94 | 92 | 69 |
丙 | 81 | 84 | 78 |
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序;
(2)该单位规定:笔试、面试、体能分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分.根据规定,请你说明谁将被录用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com