
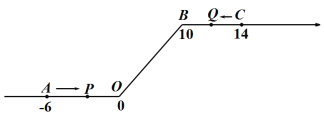
【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣6,点B表示10,点C表示14,我们称点A和点C在数轴上相距20个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.
问:
(1)动点P从点A运动至C点需要时间为 秒;P、Q两点相遇时,求出相遇点M所对应的数是 ;
(2)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
【答案】(1)15;4(2)t的值为2、3.5或5.
【解析】
(1)根据路程除以速度等于时,可得答案;根据相遇时P,Q的时间相等,可得方程,解出即可.
(2)根据PO与BQ的时间相等,可得方程,解出即可.
(1)点P运动至点C时,所需时间t=6÷2+10÷1+4÷2=15(s),
答:动点P从点A运动至C点需要15秒;
由题可知,P、Q两点相遇在线段OB上于M处,设OM=x.
则6÷2+x÷1=4÷1+(10-x)÷2,
x=4,
答:M所对应的数为4.
(2)P点运动完时间:6÷2+10÷1+4÷2=15(s)
Q点运动完时间:4÷1+10÷2+6÷1=15(s)
P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等有以下可能:
①动点Q在CB上,动点P在AO上,
则:4-1t=6-2t,解得:t=2.
②动点Q在CB上,动点P在OB上,
则:4-1t=1×(t-3),解得:t=3.5.
③动点Q在BO上,动点P在OB上,
则:2(t-4)=1×(t-3),解得:t=5.
④动点Q在OA上,动点P在OB上,
则:1×(t-9)+10=1×(t-3),无解
④动点Q在OA上,动点P在BC上,
则:1×(t-9)+10=2×(t-13)+10,解得:t=17>15,
综上所述:t的值为2、3.5或5.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:
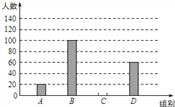
【题目】国家规定“中小学生每天在校体育活动时间不低于1小时”.为此,我区就“你每天在校体育活动时间是多少”的问题随机调查了区内300名初中学生.根据调查结果绘制成的统计图(部分)如图所示,其中分组情况是:
A组:t<0.5h B组:0.5h≤t<1h C组:1h≤t<1.5h D组:t≥1.5h
请根据上述信息解答下列问题:
(1)C组的人数是 .
(2)本次调查数据的中位数落在 组内;
(3)若我区有5400名初中学生,请你估计其中达国家规定体育活动时间的人约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个整数能表示成a2+b2(a、b是正整数)的形式,则称这个数为“完美数”。例如5是“完美数”,因为5=22+12,再如M=x2+2xy+2y2=(x+y)2 +y2(x、y是正整数),所以M也是“完美数”。
(1)请你再写一个小于10的“完美数”,并判断29是否为“完美数”;
(2)试判断(x2+9y2)(4y2+x2)(x、y是正整数)是否为“完美数”,并说明理由;
(3)已知S=x2+4y2+4x-12y+k(x、y是正整数,k是常数),要使S为“完美数”,试求出符合条件的一个k值,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个多位自然数的任意两个相邻数位上,左边数位上的数总比右边数位上的数小1,那么我们把这样的自然数叫做“相连数”,例如:234,4567,56789,......都是“相连数”.
(1)请直接写出最大的两位“相连数”与最小的三位“相连数”,并求它们的和;
(2)若某个“相连数”恰好等于其个位数的576倍,求这个“相连数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天,一蔬菜经营户用114元从蔬菜批发市场购进黄瓜和土豆共40kg到菜市场去卖,黄瓜和土豆这天的批发价好零售价(单位:元/kg)如下表所示:
品名 | 批发价 | 零售价 |
黄瓜 | 2.4 | 4 |
土豆 | 3 | 5 |
(1)他当天购进黄瓜和土豆各多少千克?
(2)如果黄瓜和土豆全部卖完,他能赚多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)
为了加强学生课外阅读,开阔视野,某校开展了“书香校园,从我做起”的主题活动.学校随机抽取了部分学生,对他们一周的课外阅读时间进行调查,绘制出频数分布表和频数分布直方图的一部分如下:


请根据图表信息回答下列问题:
(1)频数分布表中的![]() ,
,![]() ;
;
(2)将频数分布直方图补充完整;
(3)学校将每周课外阅读时间在![]() 小时以上的学生评为“阅读之星”,请你估计该校
小时以上的学生评为“阅读之星”,请你估计该校![]() 名学生中评为“阅读之星”的有多少人?
名学生中评为“阅读之星”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
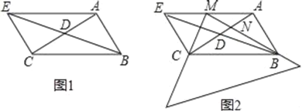
【题目】已知:如图1,Rt△ABC中,∠BAC=90°,点D是线段AC的中点,连接BD并延长至点E,使BE=2BD.连接AE,CE.
(1)求证:四边形ABCE是平行四边形;
(2)如图2所示,将三角板顶点M放在AE边上,两条直角边分别过点B和点C,若∠MEC=∠EMC,BM交AC于点N.求证:△ABN≌△MCN.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com