
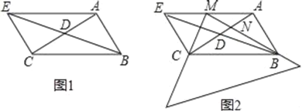
【题目】已知:如图1,Rt△ABC中,∠BAC=90°,点D是线段AC的中点,连接BD并延长至点E,使BE=2BD.连接AE,CE.
(1)求证:四边形ABCE是平行四边形;
(2)如图2所示,将三角板顶点M放在AE边上,两条直角边分别过点B和点C,若∠MEC=∠EMC,BM交AC于点N.求证:△ABN≌△MCN.
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E为 BC上的点,F为 CD边上的点,且AE=AF,AB=4,设EC=x,△AEF 的面积为y,则y与x之间的函数关系式是____.

查看答案和解析>>
科目:初中数学 来源: 题型:
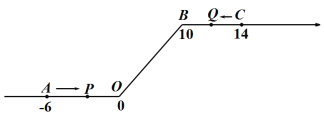
【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣6,点B表示10,点C表示14,我们称点A和点C在数轴上相距20个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.
问:
(1)动点P从点A运动至C点需要时间为 秒;P、Q两点相遇时,求出相遇点M所对应的数是 ;
(2)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
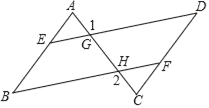
【题目】在括号内注明说理依据.如图已知∠B=∠D,∠1=∠2,试猜想∠A与∠C的大小关系,并说明理由.
解:猜想∠A=∠C
∵∠1=∠2 (已知)
∠1=∠EGC
∴∠2=∠EGC
∴BF∥DE
∴∠B=∠AED
∵∠B=∠D
∴∠AED=∠D (等量代换)
∴AB∥CD
∴∠A=∠C .
查看答案和解析>>
科目:初中数学 来源: 题型:
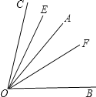
【题目】下列各小题中,都有OE平分∠AOC,OF平分∠BOC.
(1)如图,若点A.O.B在一条直线上,则∠AOB与∠EOF的数量关系是:∠AOB=_____∠EOF.
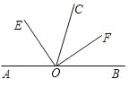
(2)如图,若点A.O.B不在一条直线上,则题(1)中的数量关系是否成立?请说明理由.
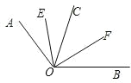
(3)如图,若OA在∠BOC的内部,则题(1)中的数量关系是否仍成立?请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
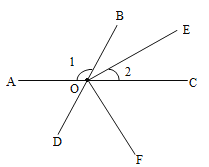
【题目】如图所示,点![]() 、
、![]() 、
、![]() 在同一直线上,
在同一直线上,![]() 是
是![]() 的平分线,
的平分线,![]() ,
,![]() ,
,![]() .
.
(1)求![]() 的度数(请写出解题过程).
的度数(请写出解题过程).
(2)如以![]() 为一边,在
为一边,在![]() 的外部画
的外部画![]() ,问边
,问边![]() 与边
与边![]() 成一直线吗?请说明理由.
成一直线吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年7月7日,国务院办公厅发布《国务院办公厅关于同意山西省承办2019年第二届全国青年运动会的函》,本届运动会初步确定在2019年8月至9月份举办,历时8至10天,预计约有55个代表团参赛,为了让每位运动员在比赛之余能有一个较好的疗养锻炼的环境,二青会筹备委员会,决定从某公司采购甲、乙两种健身器材共800件,已知购买2件甲器材与3件乙器材的价格相同,购买3件甲器材比2件乙器材的价格多1500元.
(1) 每件甲乙两种器材各多少元?
(2) 若购买甲、乙两种器材的价格不超过54万元,则最多可购买甲种器材多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于有理数a, b,规定一种新运算: a★b= 2ab-b.
(1)计算: (-3)★4=______________;
(2)若方程(x-4)★3=6,求x的值;
(3)计算: 5★[(-2)★3]的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com