
【题目】下列各小题中,都有OE平分∠AOC,OF平分∠BOC.
(1)如图,若点A.O.B在一条直线上,则∠AOB与∠EOF的数量关系是:∠AOB=_____∠EOF.
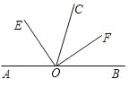
(2)如图,若点A.O.B不在一条直线上,则题(1)中的数量关系是否成立?请说明理由.
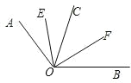
(3)如图,若OA在∠BOC的内部,则题(1)中的数量关系是否仍成立?请说明理由
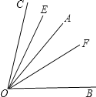
【答案】(1)2(2)成立,理由见解析(3)成立,理由见解析
【解析】
(1)根据角平分线的定义可得,∠AOB=2∠EOF;
(2)根据角平分线的定义求得∠EOF=![]() ∠AOB;
∠AOB;
(3)根据角平分线的定义求得∠EOF=∠COF∠EOC=![]() ∠AOB.
∠AOB.
(1)
∵OE平分∠AOC,OF平分∠BOC
∴∠EOF=∠EOC+∠COF=![]() ∠AOC+
∠AOC+![]() ∠BOC=
∠BOC=![]() (∠AOC+∠BOC)
(∠AOC+∠BOC)
=![]() ∠AOB
∠AOB
∴∠AOB=2∠EOF.
(2)成立,理由是:
因为OE平分∠AOC,所以∠EOC=∠AOC
因为OF平分∠BOC,所以∠COF=∠BOC
所以∠EOF=∠EOC+∠COF=![]() ∠AOC+
∠AOC+![]() ∠BOC=
∠BOC=![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ∠AOB
∠AOB
(3)成立
理由是:因为OE平分∠AOC,所以∠EOC=![]() ∠AOC
∠AOC
因为OF平分∠BOC,所以∠COF=![]() ∠BOC
∠BOC
所以∠EOF=∠COF∠EOC=![]() ∠BOC
∠BOC![]() ∠AOC
∠AOC
=![]() (∠BOC∠AOC)
(∠BOC∠AOC)
=![]() ∠AOB
∠AOB
所以∠AOB=2∠EOF.


科目:初中数学 来源: 题型:
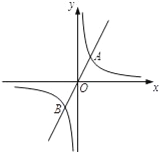
【题目】如图,正比例函数y=2x的图象与反比例函数y=![]() 的图象交于点A、B,AB=2
的图象交于点A、B,AB=2![]() ,
,
(1)求k的值;
(2)若反比例函数y=![]() 的图象上存在一点C,则当△ABC为直角三角形,请直接写出点C的坐标.
的图象上存在一点C,则当△ABC为直角三角形,请直接写出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天,一蔬菜经营户用114元从蔬菜批发市场购进黄瓜和土豆共40kg到菜市场去卖,黄瓜和土豆这天的批发价好零售价(单位:元/kg)如下表所示:
品名 | 批发价 | 零售价 |
黄瓜 | 2.4 | 4 |
土豆 | 3 | 5 |
(1)他当天购进黄瓜和土豆各多少千克?
(2)如果黄瓜和土豆全部卖完,他能赚多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发门市销售两种商品,甲种商品每件售价为300元,乙种商品每件售价为80元.新年来临之际,该门市为促销制定了两种优惠方案:
方案一:买一件甲种商品就赠送一件乙种商品;
方案二:按购买金额打八折付款.
某公司为奖励员工,购买了甲种商品20件,乙种商品x(x≥20)件.
(1)分别写出优惠方案一购买费用y1(元)、优惠方案二购买费用y2(元)与所买乙种商品x(件)之间的函数关系式;
(2)若该公司共需要甲种商品20件,乙种商品40件.设按照方案一的优惠办法购买了m件甲种商品,其余按方案二的优惠办法购买.请你写出总费用w与m之间的关系式;利用w与m之间的关系式说明怎样购买最实惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
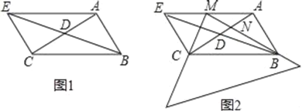
【题目】已知:如图1,Rt△ABC中,∠BAC=90°,点D是线段AC的中点,连接BD并延长至点E,使BE=2BD.连接AE,CE.
(1)求证:四边形ABCE是平行四边形;
(2)如图2所示,将三角板顶点M放在AE边上,两条直角边分别过点B和点C,若∠MEC=∠EMC,BM交AC于点N.求证:△ABN≌△MCN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年5月14日至15日,“一带一路”国际合作高峰论坛在北京举行,本届论坛期间,中国同30多个国家签署经贸合作协议,某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区. 已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.
(1)甲种商品与乙种商品的销售单价各多少元?
(2)若甲、乙两种商品的销售总收入不低于5400万元,则至少销售甲种商品多少万件?
查看答案和解析>>
科目:初中数学 来源: 题型:
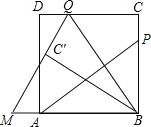
【题目】如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.
(1)试探究AP与BQ的数量关系,并证明你的结论;
(2)当AB=3,BP=2PC,求QM的长;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,锐角△ABC内接于⊙O,若⊙O的半径为6,sinA=![]() ,求BC的长.
,求BC的长.

【答案】BC=8.
【解析】试题分析:通过作辅助线构成直角三角形,再利用三角函数知识进行求解.
试题解析:作⊙O的直径CD,连接BD,则CD=2×6=12.
∵![]()
∴![]()
∴![]()

点睛:直径所对的圆周角是直角.
【题型】解答题
【结束】
22
【题目】如图,一次函数y=k1x+b与反比例函数y=![]() 的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式k1x+b>![]() 的解集;
的解集;
(3)若P(p,y1),Q(﹣2,y2)是函数y=![]() 图象上的两点,且y1≥y2,求实数p的取值范围.
图象上的两点,且y1≥y2,求实数p的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表给出了代数式﹣x2+bx+c与x的一些对应值:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
﹣x2+bx+c | … | 5 | n | c | 2 | ﹣3 | ﹣10 | … |
(1)根据表格中的数据,确定b,c,n的值;
(2)设y=﹣x2+bx+c,直接写出0≤x≤2时y的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com