
����Ŀ��2019��7��7�գ�����Ժ�칫������������Ժ�칫������ͬ��ɽ��ʡ�а�2019��ڶ���ȫ�������˶���ĺ����������˶������ȷ����2019��8����9�·ݾٰ죬��ʱ8��10�죬Ԥ��Լ��55�������Ų�����Ϊ����ÿλ�˶�Ա�ڱ���֮������һ���Ϻõ����������Ļ����������ﱸίԱ�ᣬ������ij��˾�ɹ��ס������ֽ������Ĺ�800������֪����2����������3�������ĵļ۸���ͬ������3�������ı�2�������ĵļ۸��1500Ԫ.
(1) ÿ�������������ĸ�����Ԫ��
(2) ������ס����������ĵļ۸���54��Ԫ�������ɹ���������Ķ��ټ���
���𰸡���1��900,600����2��200.
��������
��1����ÿ���������ļ۸�ΪxԪ��ÿ���������ļ۸�ΪyԪ�������⡰����2����������3�������ĵļ۸���ͬ������3�������ı�2�������ĵļ۸��1500Ԫ����
![]() �����㼴�ɵõ��𰸣�
�����㼴�ɵõ��𰸣�
��2����������Ĺ�����m�������������Ĺ����ˣ�800-m����.������ã� 900m+600(800-m)��540000�����㼴�ɵõ���.
�⣨1����ÿ���������ļ۸�ΪxԪ��ÿ���������ļ۸�ΪyԪ��������ã�
![]()
��ã�![]()
��ÿ�������������ĸ�900Ԫ��600Ԫ.
��2����������Ĺ�����m�������������Ĺ����ˣ�800-m����.������ã�
900m+600(800-m)��540000
��ã�m��200
�𣺹������������200��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������ܱ�ʾ��a2��b2��a��b��������������ʽ����������Ϊ����������������5�ǡ�������������Ϊ5��22��12������M��x2��2xy��2y2=(x��y)2 ��y2��x��y����������������MҲ�ǡ�����������
��1��������дһ��С��10�ġ��������������ж�29�Ƿ�Ϊ������������
��2�����ж�(x2��9y2)(4y2��x2)��x��y�����������Ƿ�Ϊ��������������˵�����ɣ�
��3����֪S��x2��4y2��4x��12y��k��x��y����������k�dz�������ҪʹSΪ���������������������������һ��kֵ����˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
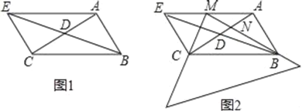
����Ŀ����֪����ͼ1��Rt��ABC�У���BAC��90������D���߶�AC���е㣬����BD���ӳ�����E��ʹBE��2BD������AE��CE��
��1����֤���ı���ABCE��ƽ���ı��Σ�
��2����ͼ2��ʾ�������ǰ嶥��M����AE���ϣ�����ֱ�DZ߷ֱ����B�͵�C������MEC����EMC��BM��AC�ڵ�N����֤����ABN�ա�MCN��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
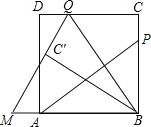
����Ŀ����ͼ��PΪ������ABCD�ı�BC��һ����(P��B��C���غ�)������AP������B��BQ��AP��CD�ڵ�Q������BQC��BQ���ڵ�ֱ�߶��۵õ���BQC�����ӳ�QC����BA���ӳ����ڵ�M��
(1)��̽��AP��BQ��������ϵ����֤����Ľ��ۣ�
(2)��AB=3��BP=2PC����QM�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
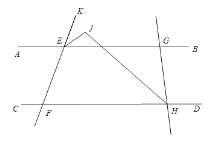
����Ŀ����ͼ1��ֱ��AB��CD��ֱ��EF��AB�ڵ�E����CD�ڵ�F����G�͵�H�ֱ���ֱ��AB��CD�ϵĶ��㣬��ֱ��GH��EIƽ����AEF��HIƽ����CHG��EI��HI���ڵ�I.
��1����ͼ����G�ڵ�E����࣬��H�ڵ�F���Ҳ࣬����AEF=70�㣬��CHG=60�㣬���ETH�Ķ���.
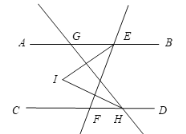
��2����ͼ����G�ڵ�E���Ҳ࣬��HҲ�ڵ�F���Ҳ࣬����AEF=![]() ����CHG=���������������䣬���ETH�Ķ���.
����CHG=���������������䣬���ETH�Ķ���.
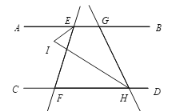
��3����ͼ����G�ڵ�E���Ҳ࣬��HҲ�ڵ�F���Ҳ࣬��GHC��ƽ����HJ����KEG��ƽ����EJ�ڵ�J.�����������䣬����AEF=![]() ����CHG=�������EJH�Ķ���.
����CHG=�������EJH�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ABC�ڽ�����O������O�İ뾶Ϊ6��sinA=![]() ����BC�ij���
����BC�ij���

���𰸡�BC=8��
�����������������ͨ���������߹���ֱ�������Σ����������Ǻ���֪ʶ������⣮
�������������O��ֱ��CD������BD����CD=2��6=12.
��![]()
��![]()
��![]()

�㾦��ֱ�����Ե�Բ�ܽ���ֱ��.
�����͡������
��������
22
����Ŀ����ͼ��һ�κ���y=k1x+b�뷴��������y=![]() ��ͼ����A��2��m����B��n����2�����㣮����B��BC��x�ᣬ����ΪC����S��ABC=5��
��ͼ����A��2��m����B��n����2�����㣮����B��BC��x�ᣬ����ΪC����S��ABC=5��
��1����һ�κ����뷴���������Ľ���ʽ��
��2������������������ֱ��д������ʽk1x+b��![]() �Ľ⼯��
�Ľ⼯��
��3����P��p��y1����Q����2��y2���Ǻ���y=![]() ͼ���ϵ����㣬��y1��y2����ʵ��p��ȡֵ��Χ��
ͼ���ϵ����㣬��y1��y2����ʵ��p��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
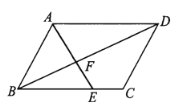
����Ŀ����ͼ,ƽ���ı���![]() ��,��
��,��![]() Ϊ
Ϊ![]() ����һ��,
����һ��, ![]() ��
��![]() ���ڵ�
���ڵ�![]() ,��֪
,��֪![]() ���������6,
���������6, ![]() ���������4,���ı���
���������4,���ı���![]() ���������__________��
���������__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
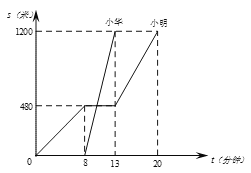
����Ŀ��С����С����ͬ��ͬѧ��Ҳ���ھӣ�ij���糿��С��7��40�ȳ���ȥѧУ������һ�κ���;��ͣ�³�����ͣ�����������ѧʱ��쵽�ˣ����ܲ���ѧУ��С����Һ�ֱ�ӳ˹�����������ѧУ����ͼ�����ǴӼҵ�ѧУ���ߵ�·��s���ף�������ʱ��t�����ӣ��Ĺ�ϵͼ��������˵����
��С������ѧУ�ľ���1200�ף�
��С�����������������ٶ���240��/�֣�
������������������7:50����������
��С���ij���ʱ�䲻�䣬��С���ɳ˹���������Ϊ�ܲ������ܲ����ٶ���100��/��ʱ�����ǿ���ͬʱ����ѧУ.������ȷ�ĸ����ǣ� ��
A. 1 ��B. 2��
C. 3 ��D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
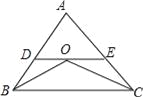
����Ŀ����֪����ͼ����ABC�У�BO��CO�ֱ��ǡ�ABC�͡�ACB��ƽ���ߣ���O���ֱ�߷ֱ�AB��AC�ڵ�D��E����DE��BC����AB=6 cm��AC=8 cm�����ADE���ܳ�Ϊ__________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com