练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

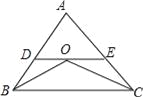
    【题目】已知：如图，△ABC中，BO，CO分别是∠ABC和∠ACB的平分线，过O点的直线分别交AB、AC于点D、E，且DE∥BC．若AB=6 cm，AC=8 cm，则△ADE的周长为__________．

    【答案】14cm

    【解析】

    两直线平行，内错角相等，以及根据角平分线性质，可得△OBD、△EOC均为等腰三角形，由此把△AEF的周长转化为AC+AB．

    解：∵DE∥BC，∴∠DOB=∠OBC，又∵BO是∠ABC的角平分线，∴∠DBO=∠OBC，∴∠DBO=∠DOB，∴BD=OD，同理：OE=EC，

    ∴△ADE的周长=AD+OD+OE+EC=AD+BD+AE+EC=AB+AC=14cm．

    答案是：14cm．

    “点睛”本题考查了平行线的性质和等腰三角形的判定及性质，正确证明△OBD、△EOC均为等腰三角形是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】2019年7月7日，国务院办公厅发布《国务院办公厅关于同意山西省承办2019年第二届全国青年运动会的函》，本届运动会初步确定在2019年8月至9月份举办，历时8至10天，预计约有55个代表团参赛，为了让每位运动员在比赛之余能有一个较好的疗养锻炼的环境，二青会筹备委员会，决定从某公司采购甲、乙两种健身器材共800件，已知购买2件甲器材与3件乙器材的价格相同，购买3件甲器材比2件乙器材的价格多1500元.

    (1) 每件甲乙两种器材各多少元？

    (2) 若购买甲、乙两种器材的价格不超过54万元，则最多可购买甲种器材多少件？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于有理数a, b,规定一种新运算: a★b= 2ab-b.

    (1)计算: (－3)★4=______________；

    (2)若方程(x-4)★3=6，求x的值;

    (3)计算: 5★[(-2)★3]的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将一条数轴在原点O和点B处各折一下，得到一条“折线数轴”．图中点A表示﹣11，点B表示10，点C表示18，我们称点A和点C在数轴上相距29个长度单位．动点P从点A出发，以2单位/秒的速度沿着“折线数轴”的正方向运动，从点O运动到点B期间速度变为原来的一半，之后立刻恢复原速；同时，动点Q从点C出发，以1单位/秒的速度沿着数轴的负方向运动，从点B运动到点O期间速度变为原来的两倍，之后也立刻恢复原速．设运动的时间为t秒．

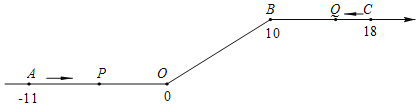
    问：（1）动点P从点A运动至C点需要多少时间？

    （2）P、Q两点相遇时，求出相遇点M所对应的数是多少；

    （3）求当t为何值时，P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，将正方形ABCD置于平面直角坐标系中，其中AD边在x轴上，其余各边均与坐标轴平行，直线l：y＝x﹣3沿x轴的负方向以每秒1个单位的速度平移，在平移的过程中，该直线被正方形ABCD的边所截得的线段长为m，平移的时间为t（秒），m与t的函数图象如图2所示，则图2中b的值为（ ）

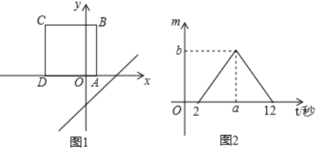
    A. 5B. 4C. 3D. 2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正的边长为2，过点的直线，且与关于直线对称.

    （Ⅰ）连接，判断四边形的形状并进行证明.

    （Ⅱ）为线段上一动点，求的最小值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】现定义运算：对于任意有理数a、b，都有ab＝ab－b，如：23＝2×3－3，请根据以上定义解答下列各题：

    （1） 2（－3）＝___________，x（－2）＝___________；

    （2） 化简：[（－x）3] （－2）；

    （3） 若x ＝3（－x），求x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】长为1，宽为a的矩形纸片（），如图那样折一下，剪下一个边长等于矩形宽度的正方形（称为第一次操作）；再把剩下的矩形如图那样折一下，剪下一个边长等于此时矩形宽度的正方形（称为第二次操作）；如此反复操作下去．若在第n此操作后，剩下的矩形为正方形，则操作终止．当n=3时，a的值为（ ）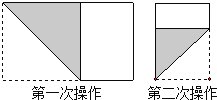

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了推动我区教育教学发展，加快教师的成长与提升，2018-2019学年度某名师工作室开展了多次送教下乡活动.在某次研讨课活动中,为了分析某节复习课的教学效果，课前,张老师让八()班每位同学做道类似题目(与这节课内容相关)析某节复至少容对,解题情况如图所示:课后，再让学生做道类似的题目.结果如表所示.已知每位学生至少答对题.

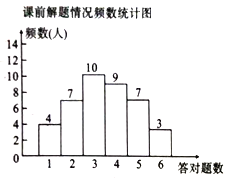
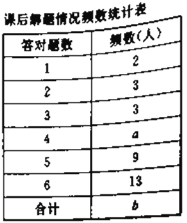
    （1）根据图表信息填空： ； .

    （2）该班课前解题时答对题数的众数是 ；课后答对题数的中位数是 .

    （3）通过计算课前，课后学生答对题数的平均数，评价这节复习课的教学效果.

    查看答案和解析>>

    同步练习册答案